「干货」开关电源RC吸收电路的分析

01 问题背景

我们常用的AC-DC开关电源中，由于初级线圈的漏感而再次级线圈上产生的瞬间反向脉冲是非常严重的。如下图图1，这是用MPS公司的MP020-5芯片搭建的AC-DC电路，这里测的是次级部分肖特基二极管两端的波形。我们知道，肖特基二极管的最大的作用就是防止变压器初级线圈的瞬态反向脉冲通过次级线圈对后级电路造成冲击，如果在芯片启动之后，后级肖特基二极管因为无法承受反向冲击脉冲而造成短路，那么开关电源芯片会被瞬间击穿。这里我是用的变压器初级次级比值为1：3，而我们一般的反向瞬间脉冲约为700~1000V，甚至更多，我们根实际测得的波形可以看出，次级线圈的最大反向脉冲电压为224V左右。我们在很多的AC-DC电源方案中都可以看到肖特基二极管并联一个RC电路，但是我们不知道这两个元器件的值怎么去选，因为实际的设计中，我们不一定会按照方案中要求去选用一模一样的变压器，就比如MPS020-5推荐的变压器匝数比为1：11，但是考虑到实际变压器的体积，我们改为1：3，那么这个匝数比的改变会导致次级反向瞬间脉冲的不同，那么对于肖特基二极管的反向承受电压就有一个严格的要求。那么如何能让RC真正的起到作用而减少肖特基二极管的成本，或者说这个RC到底起一个什么作用。本文以实验的角度和大家一起讨论这个问题。

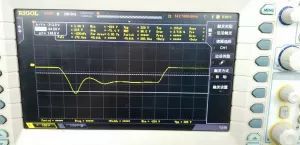
图1

附：MP020-5开关电源原理图

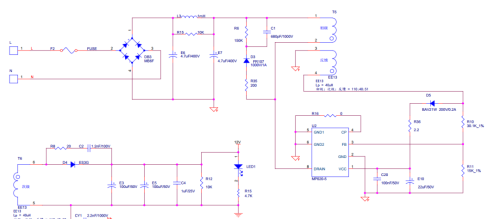
图2

02 分析问题

从系统控制理论的角度出发，我们将这个次级的电路进行模型化，如图3和图4。

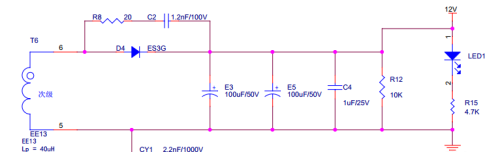
图3

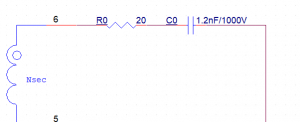
图4

这里由于电容具有开关电源开启瞬间短路的性质，所以R12和R15的后级都被短路了，等效电容C0为E3、E5电容并联再与C2串联。而电容串联的计算是等效为电阻并联的计算，即串联的电容越小，等效电容越小，所以我们直接按最小的电容C2进行计算，即等效电容C0为1.2nF，电感为变压器的次级线圈，电阻R8（等效电阻为R0）为我们需要测定的值。

根据基尔霍夫电压定律写出RLC串联谐振的微分方程，再进行拉普拉斯变化可以看出，这个模型我们可以发现这是一个RLC串联谐振电路，在控制系统中这是一个典型的二阶系统，具体的公式推导见图5和图6。

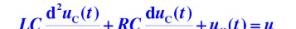
图5

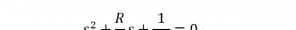
图6

这是一个典型的二阶连续系统，我们再次审视这个波形图图7可以发现，这是一个瞬态响应图像。瞬态响应即在开关电源开启的瞬间产生的响应。

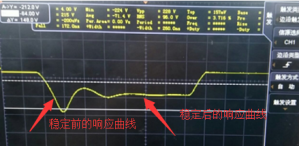
图7

二阶系统下，瞬态响应主要表现为三种状态：欠阻尼、临界阻尼、过阻尼。

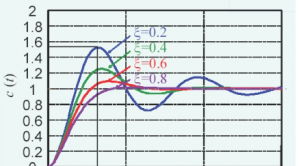
欠阻尼响应的曲线图 图8

欠阻尼由于阻尼不够，系统在响应瞬间会超过稳态值，然后慢慢的通过振荡来跌落到稳态值，上图的曲线表现出来的就是欠阻尼的状态。也就是说，我们的电压本来应该达不到224V，但是在一个惯性的作用下，系统在达到了稳定值之后超过了稳定值，达到了一个最大值，然后慢慢落下维持在稳定值的范围内。

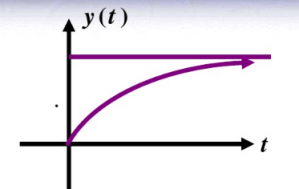
临界阻尼响应的曲线图 图9

临界阻尼下由于阻尼刚刚够，系统在响应瞬间慢慢的上升到稳态值，不会产生惯性，我们的所需要的就是这样一种波形。RLC串联谐振的拉普拉斯变换公式推导如图图10。

图10

我们通过电桥测得L的值为260mH，L的值为变压器次级线圈的电感值，C为1.2nF，带入求出电阻R为1658Ω。

03 测试验证

根据得到的理论值可以得到在1658欧姆左右可以达到临界阻尼，由于实际中手边没有1658欧姆的电阻，最大只有357欧姆，而焊盘只够放两个电阻串联，所以我将两个357欧姆的电阻串联得到714欧姆的电阻，然后将电路进行测试，下图为测得的波形图图11。

可以看出系统在响应瞬间就很快的达到了稳态，而之前出现的欠阻尼的冲击脉冲也被消除了，而反向电压也被钳制在-156V，当然了这个阻值不能太大，在达到一定的值之后，系统会越过临界阻尼，这个电阻的选值是一个范围。另外还有一个就是这里的电容也要尽量的小，在nF级，如果太大会造成芯片爆炸。总的来说，在确定好RC的值之后，我们可以有效的抑制次级反向脉冲由于惯性对肖特基二极管造成的更大的电压冲击。这样做的好处可以让我们理解RC存在的理由，当然还可以节约物料成本。之前使用的物料为SS320肖特基二极管，反向承受电压为200V，经常爆板，后来使用了ES3G，反向承受电压为400V，虽然可以用但是物料比较贵。通过这种简单的办法可以更好的节约成本。

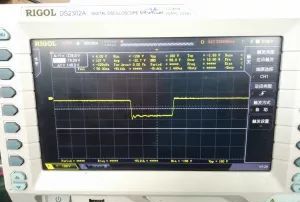
图11

免责声明：本文转自网络，版权归原作者所有，如涉及作品版权问题，请及时与我们联系，谢谢！