极性与非极性电容并联的作用

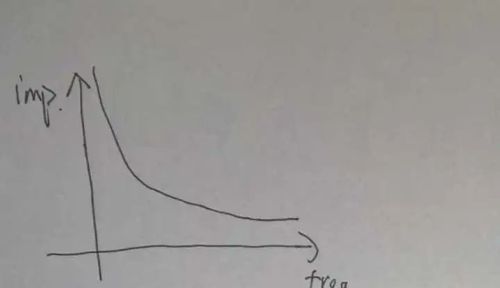
这个也是理想的电源网络应该有的阻抗特性样子。而实际的电容，会有引脚和自身材料特性带来的等效串联电感（ESL），所以曲线会变成这幅鬼样。

电解电容值很大，但同时ESL也非常大，所以用它来做低频上的去耦工作。但是在高频段，因为很大的ESL，这时候电解电容的“电感特性”占了主导地位，频率越高去耦效果越弱。有时电路中也会利用大容值电解电容来抚平极低频段的电压波动，这时更加多地是在利用电容的储能特性（你也可以多掏点钱用线性稳压器来解决这个问题），而不是狭义上的“去耦”或者“滤波”了。

瓷片电容来说虽然容值较小，在低频段的去耦效果不明显，但是相对较小的ESL使得它在高频段特定范围内的去耦效果非常不错。

因此，最好的办法就是把这两个电容并联来用。一并起来，阻抗曲线大概就会变成这个样子。

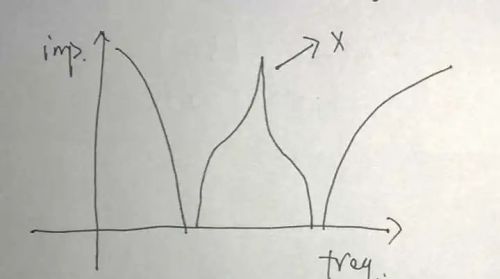
这个理想电容模型的阻抗曲线因为忽略了ESR，显得非常奇怪，既有尖峰也有为负的阻抗。如果考虑阻抗的相频特性，在阻抗接近0的时候这个电路组合甚至会发生谐振。所以考察这个问题必须要电容的ESR加进来，如下列形式的电路。

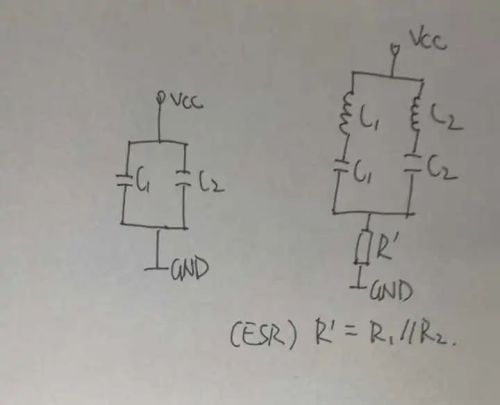
然后阻抗特性就会变成这样了。

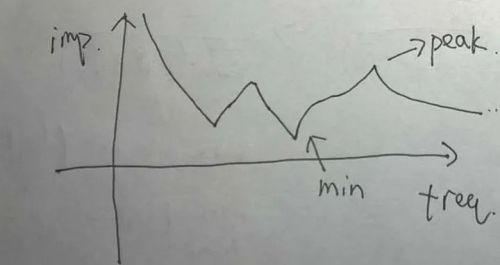
像上图展示的一样，这个阻抗特性曲线虽然也有明显尖锐的峰值和谷值，但是从整体上看，明显比上图平滑了很多。峰值部分一般称为“抗谐振”点（anti-resonance）。既然求电容组合要发挥去耦的作用，那设计要点之一就是这个尖峰必须远离电路中的噪声频率分布集中点。而逆向利用这个尖峰的思路就是把这个峰值尽量靠近临近负载电流谱频率集中点上，尽量减少电路拓扑上的相邻负载变化对本地电压的影响。

题主的原理图中和去耦网络相连的是REF脚，一般都是指参考信号输入。没有更多信息，那我就假设一个场景来举例说明上图中谷值的意义。假设这是一个ADC的REF引脚，ADC每一个conversion周期都会从REF脚吸取一次或多次电流，具体取决于ADC的电路结构。在这种情况下，REF的电流谱是有规律可循的。我们希望REF脚在工作过程中电压的波动尽可能少，那就可以将去耦网络的谷值尽量靠近这个电流谱中的频率集中点。因为谷值min比ESR值R' 要小，在这个频率上电源网络对电流信号的阻抗是最低的。这是设计要点之二。

这里还有一个不得不提的问题，就是由去耦网络带来潜在的谐振危险。虽然去耦网络的阻抗在考虑了ESR之后谷值已经不为0了，但是在很多电路中，这个谷值的数值还是相当低的。再加上去耦网络的另一头就是电源，尽量减少谐振的发生几率几乎成了Design Rule的标配。至于如何消除谐振，又是另一个复杂的话题了。

总结一下，一大一小不同种类的电容并联，可以用“高低搭配”的方法通俗解释。但是严谨说来，尤其是对于简单的数字电路，工作过程中电流谱有明显规律的，相比使用单一电容的结构，两个电容并联的组合在成本最优的前提下提供了大量的优化空间（一大一小的ESR和ESL组合）。

上面的都是在理论上泛泛而谈，实际上这个优化做起来是非常困难的。主要是电路中影响ESL的参数实在太多了，便宜的电解电容“体质”严重不一致使得ESL的失配分析做起来很麻烦。一句话总结就是很难将理论计算结果与做出来的电路对应起来。

对于没有明显频率分布的电路电流谱，又怎么办呢？最简单的办法就是多并不同参数不同规格材料的电容呗，让这个特性曲线不断逼近设计需求的“平坦状态”。

电源完整性（Power Integrity）就是系统研究这类问题的。

免责声明：本文转自网络，版权归原作者所有，如涉及作品版权问题，请及时与我们联系，谢谢！