开关电容采样系统中的热噪声以及过采样如何影响热噪声

开关电容采样kT/C噪声和一阶RC kT/C噪声的区分

最初学习噪声时，首先学到的是，一阶RC电路中输出端的总积分噪声（功率）可以被表示为kT/C。之后，学习到开关电容采样电路采样得到的噪声功率也为kT/C。然而，需要注意的是，两者虽然在数值上相等，但得到该数值的过程却大不相同。开关电容采样电路在开关闭合时自然是一个一阶RC网络，但当其被采样时，必然存在着频谱的搬移过程，最终得到的采样后的热噪声，其实是频谱搬移后的结果。简而言之：

一阶RC kT/C是一个连续时间工作的热噪声；开关电容采样 kT/C是一个离散的，对RC网络热噪声进行一系列采样，频谱搬移后形成的热噪声；后者是前者采样后的结果。

那么问题来了：

后者是经过前者怎样的过程得到的？为何两者数值相等？

首先我们定义一个重要概念，噪声的等效带宽BWn。EEE598中对其定义如下图所示：

等效带宽的引入是为了将噪声的频谱图简化为一个更规则的长方形，这样我们在进行频谱搬移时可以更为方便地进行计算。

其次，我们需要明确，在开关电容采样时，采样频率fs<<BWn，这是因为，为了采样时输入信号可以在采样电容上充分建立，开关电容的时间常数是远小于采样时间的。

在上述情况下，采样会导致噪声在±fs的正数倍处出现交叠，如下图所示：

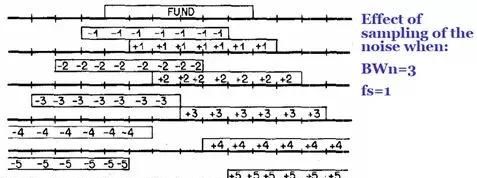
噪声被采样时频谱搬移图

将上图所有的频谱进行合并，可得到下图：

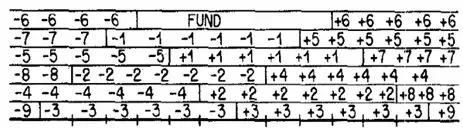
噪声被采样后噪声交叠情况

在fs内，交叠的噪声的个数为式(1)：

原本RC网络热噪声的谱密度为式(2);

噪声采样交叠后的谱密度为式(3)：

那么，在Nyquist带宽fs/2内，积分噪声为式(4)：

从式(4)可以看出：

采样后Nyquist带宽内的积分噪声值也为kT/C,但和RC网络的kT/C噪声由来不同，仅仅是数值的相等；最终的积分噪声值和fs，BWn没有关系；采样后噪声的谱密度和fs成反比。

过采样为什么可以降低热噪声

那么如何理解过采样可以降低带内噪声呢？本文通过下述两种方式理解：

根据式(4)可知，采样后fs/2内的积分噪声值和fs和BWn没有关系，恒定为kT/C。在过采样时，提高过采样率也就是提高fs不会改变总的积分噪声值，但由于热噪声是白噪声，噪声在各个频率上均匀分布，因此提高fs使得噪声的谱密度减小，fs提高N倍对应噪声谱密度减小N倍，由于信号带宽fb是恒定的，因此带宽内的积分噪声减小N倍。根据式(3)可知，采样后的噪声谱密度和fs成反比，因此fs提高N倍对应噪声谱密度减小N倍（可以理解为相同的BWn下，更大的fs让交叠的噪声数目减小），由于信号带宽fb是恒定的，因此带宽内的积分噪声减小N倍。

上述两种理解方式其实是殊途同归，前者基于fs/2内积分噪声恒定为kT/C，即式(4)出发，后者直接基于从采样后噪声混叠形成的噪声谱密度，即式(3)出发，但最终都可得到相同的结论。

该内容是小编转载自臣扬，仅供学习交流使用，如有侵权，请联系删除