信号完整性基础：为什么会有串扰？

一，为什么会有串扰

宇宙中的任何事物，只要是存在就会与万物之间发生联系，传输线也一样，世界上不存在不受任何干扰的理想传输线，它与其它千千万万的电磁信号产生着联动（电磁力的作用距离是无限远）。

传输线A是通过什么途径影响到传输线B的？通过前面章节的分析，我们知道完整的传输线模型是：电阻+电感并上电容和电阻（电导）；当两条传输线相互靠近，模型中的哪些因素会相互影响呢？

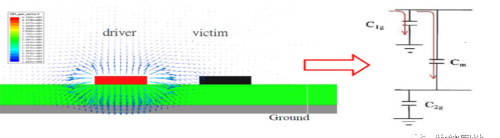
1. 任何两个具有不同电位的导体之间都会产生电容，即两个不同电位的导体之间存在一个电场。同理传输线A与传输线B之间也存在电容（传输线A、B之间的寄生电容），这就是互容（Cm）；传输线A与传输线B之间的电压（电场）变化，符合电容的充放电模型，相当于从传输线A通过互容Cm注入电流Im到传输线B；

——电容充电电流：Im = Cm*dVa/dt = Cm*ΔV/Tr；可得容性串扰=ΔVb/ΔV = (Im*Rb)/ ΔV = Cm*(ΔV/Tr)*Rb/ΔV = Cm*Rb/Tr。

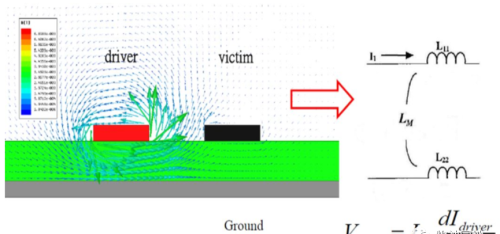
2. 之前章节我们已了解了互感：只要存在两个电流回路，就会有互感：一个回路的电路产生一个磁场，该磁场会影响第二个回路；传输线A电流变化通过互感Lm在传输线B上产生感应电压Vb；

——互感感应电压：Vb = Lm*dIa/dt = Lm*(ΔV/Ra)/Tr = Lm*ΔV/(Ra*Tr)；可得感性串扰 = ΔVb/ΔV = Lm* ΔV/(Ra*Tr*ΔV) = Lm/(Ra*Tr)。

2. 传输线A和B之间的漏电流非常小（电阻非常大），在实际应用中忽略不计，所以传输线之间的串扰分为两类：容性串扰和感性串扰。

3. 从传输线的定义出发：传输线是信号路径和回流路径组成的；所以容性串扰和感性串扰也需要考虑信号路径和回流路径。

1, 对于容性串扰来说，信号路径电平会发生变化，但是回流路径一般是GND或VCC并不会出现跳变，所以传输线之间的互容指的是：信号路径之间的寄生电容。

——如下图所示，对于共同参考平面来说，传输线A和B的回流路径是同一个导体，不存在互容。

2, 对于感性串扰来说，也同样是要考虑信号路径和回流路径，所以传输线A与传输线B之间的互感指的是：传输线A和B回路电感之间的耦合电感。

——如下图所示，对于感性串扰，需要考虑传输线的回路电感：信号路径与回流路径构成的圈圈，它们之间的耦合大小。

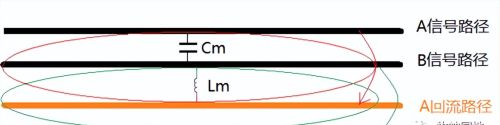
如下图所示，那么两条传输线之间的容性和感性串扰的大小与什么有关？

1. 与传输线之间的距离成反比；

——要减小互感与互容，需要增加传输线之间的距离。

2. 与信号与边沿变化率（1/Tr）成正比。

——信号边沿变化越快，串扰越大。

——随着频率的增加感性耦合也会增加，所以在高速电路中，一般互感的影响要大于互容。

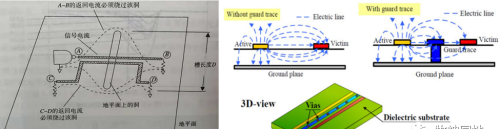
如左下图回流平面上有一条缺口（回流平面被挖空），那么传输线的回流路径就会绕过这个缺口，并导致两条传输线中信号路径与回流路径组成的回路相互重叠，互感耦合急剧增加，串扰非常大。

——举个例子，好比两个线圈之间相互重叠的面积越大，那么它们之间磁力线相互穿越的数量就越多，导致互感耦合很大；极端的情况是变压器，几乎所有的磁力线都相互穿越。

如右下图所示，两条导线都有良好参考平面，其串扰主要来自于传输线之间的互容和互感耦合；平行走线间距以及平行走线距离都影响到了串扰的大小，如果在两条导线中间增加良好的GND隔离（间隔一段距离打地孔），那么对串扰有非常好的屏蔽作用。

那如果不加中间屏蔽GND线，串扰有多大呢？下面章节详细分析。

二，容性耦合和感性耦合

1，容性耦合

上面分析了两条传输线之间的容性耦合指的是：两条信号路径之间的寄生电容相互作用。如下左图所示在动态线上传输一个高电平（上升沿）信号，将会有电流从动态线上通过C12电容不断流向静态线（耦合电流）：I12 = C12*ΔV/Tr。

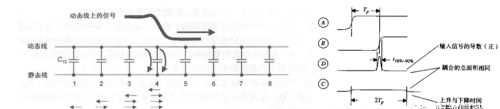
信号上升边沿越快，则dV/dt越大，我们可能认为容性耦合电流也越大？

但事实上容性耦合噪声总量与上升边沿时间无关，因为上升边沿越快，存在dV/dt的耦合区域的电容就越小（信号边沿所对应的传输线长度越短），所以容性耦合电流只与单位长度互容（Cm）有关：I12 = C12*ΔV/Tr = Cm*v*Tr*V/Tr= Cm * ν * V。（ν：光速）

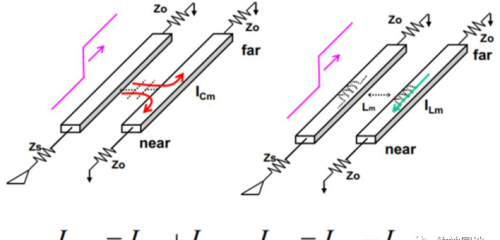
1. 耦合瞬间电流的远端（动态线终端，即前向）和近端（动态线源端，即后向）电流相等，所以耦合远端和近端电流的总面积相同（耦合能量相同）；

——如上右图所示，当信号从源端传输至终端，在整个过程中静态线近端和远端所受到的电流耦合总面积相同，只是一个扁平，另一个是脉冲信号。

2. 互容远端耦合脉冲类似输入信号的导数，随着平行走线长度的增加而变大，极性是正的。

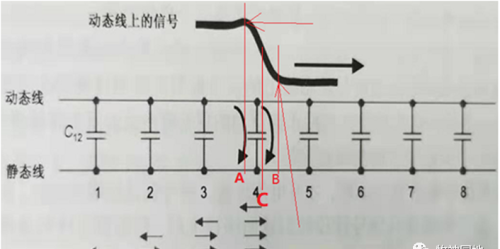
——如上右图所示，耦合电容导致的耦合电压是正的；如下图所示，因为当动态线信号由低变高时，静态线会通过耦合电容Cm对动态线进行充电操作，所以在静态线的该区域形成高电平干扰。

1.1远端容性耦合

耦合电流通过耦合电容Cm从静态线流向动态线，那么它有两个方向可以逃走：1，远端；2，近端。那么电流究竟要往哪里跑呢？

我们知道，电流的路径是自己选择的，很明显电流比我要聪明和有前瞻性，但是它选择路径有一个依据是：阻抗。那它跑到静态线后，左右（远端和近端）一看，艾玛，一样的啊。那就分头跑吧，一路一半。所以，远端容性耦合电流的大小是耦合电流大小的一半：Ic = 1/2*I12 =1/2*C*V/Tr =1/2*Cm*Len*V/Tr。

——当然，如果它耦合过来的地方刚好是阻抗不连续点，左右看过去的阻抗不同，那么远端和近端的耦合电流大小会不同；不过我们考虑的都是理想的情况，理想：就是完美的意思。

——再深一层：传输线的信号路径和回流路径之间，肯定也是有容性耦合的，那么它的耦合电流（回流）是怎么跑呢？为什么？

静态线远端容性耦合电压传输方向，同动态线信号传输方向一致的，会相互叠加；呈现出的波形是一个脉冲：宽度为动态线边沿时间，高度与耦合距离相关。

——举例子环节，如下图动态线上信号从左往右传，而静态上的容性串扰兵分两路：一个从左往右，另一个从右往左；那么从左往右这路串扰就跟动态线上信号跑的方向一样了，而且它们在同一个环境下（介电常数和磁导率一样），所以信号传输速率也一样，所以导致了远端串扰幅度就不断被叠加。

好，接下来还有两个问题，我们想清楚了就可以完全理解远端耦合的问题了；

1. 在静态线上测试到的耦合电压是如何形成的？

——我们一直在说电容耦合是由电流从动态线注入到了静态线而产生了串扰，但实际上，我们所看到的是电压而并非电流啊；即，我们只能看到静态线上信号电压的变化。

1, 首先，容性串扰电压是因为有容性耦合电流，根据欧姆定理，V = I*R，可得：远端耦合电压Vm = 远端耦合电流 * 静态线阻抗 = Ic * Z2 = 1/2*Cm*Len*(V/Tr)*Z2；

——这里再强调下，对于高频信号来说：导线不再是0Ω，而是有特征阻抗的；至于频率高到多少才不是0Ω呢？请回顾集总和分布模型，以及传输线的定义。

2, 如下图所示动态线从源端向终端发送一个上升沿信号：A点之前位置的电场已经建立完成（动态线相对于静态线的电压已无变化，不再充电），而B点之后位置电场还没开始建立，只有A与B之间位置的电场正在建立过程中（动态线相对于静态线的电压有变化），这部分的动态线与静态线还在充电；

——举个例子，A点电压从0V到V动态变化的这段时间（上升边沿）会有充电的动作形成电流，电流总量固定（电压变化是固定的），且每个时刻从静态线A点流出的电流固定不变（假设上升边沿斜率不变）；静态线A点流出的电流（电压）分别向远端和近端传输，静态线上串扰信号以光速传播。

3, 总结如上分析：任何一个点，例如C点，从动态线耦合到静态线的电流，总共经历了Tr时间，瞬时电流大小为：IC。

——随着动态线上信号的传输，静态线上信号也同步在传输，我们观察当前在C点的电流，除了C点本身耦合的电流外，还有从静态线其它位置传输并叠加的电流。

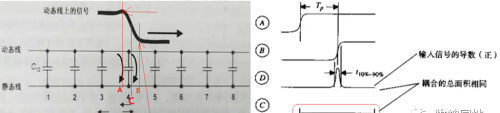
2. 为什么容性远端耦合会出现脉冲波形电压，而且脉冲宽度刚好等于边沿时间Tr？接下来根据上图的三个位置分析远端耦合是怎么叠加的：

1, 首先，我们来看B点位置，它处于动态线信号传输的最前端（波前），而静态线上的耦合信号来源于动态线，两者都以光速在沿着传输线向远端传播，所以B点也是静态线上信号传输的最前端，在B点再向右一点地方的耦合信号是0；

——可以得到结论：B点是远端耦合开始的位置，其它位置的耦合信号还没传输到B点，所以B点耦合信号 ≈ 0。

2, 再来看A点位置，这个位置处于动态线信号传播的结束点，能够叠加在A点的远端耦合信号在A点的左侧，但此时A点左侧位置的电场已经建立完成，没有电流从动态线流向静态线，所以在这个位置也没有任何叠加（静态线上耦合信号传播速度同动态线，所以远端耦合电流分布在边沿区域内）；

——得到结论：A点是远端耦合结束的位置，其它位置的耦合信号已经经过了A点（在A点右侧），A点耦合信号≈ 0。

3, 最后，我们看C点位置，这个位置处于动态信号传播的中间点，理论上C点能够叠加在C点左侧的远端耦合信号（信号向右传输），那它能够叠加多远距离的耦合信号呢？我们来想象一下：

(1) 在B点时，B点左侧是A点至B点距离的耦合信号，但这些耦合信号都还没传输到B点；

(2) 在C点时，C点处于(1/2)*Tr位置，其左侧(1/2)*Tr时间的耦合信号（A点）刚刚到达C点位置，而小于(1/2)*Tr时间距离的耦合信号都能叠加到C点；

(3) 假设D点处于C点左侧的(3/4)*Tr位置，那么按理来说在小于等于D点左侧(3/4)*Tr时间距离的耦合信号都能叠加到D点位置，但此时D点左侧只有(1/4)*Tr区域还在产生远端耦合信号，再往左侧的地方电场已经建立完成，没有耦合电流产生了。

——得到结论：在C点（(1/2)*Tr点）时，能够叠加到最大的远端耦合信号。

1.2近端容性耦合

上面已经分析了：近端容性耦合电流为什么和远端耦合电流是相等的，而且是总容性耦合电流的一半：Ic = (1/2)*I12 = (1/2)*C*ΔV/Tr = (1/2)*Cm*Len*V/Tr。但与远端耦合不同的是，当耦合长度大于饱和长度，耦合电流将达到一个饱和值（稳定值）：Ic=(1/2)* (1/2)*Cm* ν *Tr*V/Tr=(1/4)*Cm* ν *V；

1. 当耦合长度小于饱和长度，近端容性耦合电压的峰值小于饱和串扰值，实际近端容性耦合电压值与：耦合长度和饱和长度的比值成正比；

2. 近端串扰时序总时间长度时2*Td，若耦合区域时延为1ns，那么近端噪声持续时间为2ns。

——其中Td为传输线的单程线路延时；当动态线信号传输至远端时，已经过Td的时间，然而近端耦合的噪声还在远端，还需要再经过Td的时间传输回到近端，所以总时长是2*Td。

近端耦合为什么会有与远端耦合完全不同的特性呢？针对这两点特性，如下图所示，我们继续来看这张图，来分析其产生的原因：

1. 首先，我们看B点位置，在远端耦合章节说了静态线B点产生的耦合分成两部分：一半向远端传输（右侧），另一半向近端传输（左侧）；静态线B点向近端耦合的传输方向与动态线信号传输方向相反：动态线信号是从左向右传输，而静态线近端耦合信号是从右向左传输；

——B点是信号传输最远的位置，在B的右侧并没有任何近端耦合（从右往左）能够叠加到B点上，只有自己产生的耦合信号，即， B点耦合信号 ≈ 0；

2. 我们来看A点位置，此时此刻A点位置有哪些耦合信号能叠加呢？B点位置的耦合信号能叠加到A点么？

1, 静态线B点位置的耦合信号才刚刚开始产生，所以B点位置的耦合信号还需要经过Tr时间才能传输到A点，即，B点耦合信号目前不能叠加到A点耦合信号；

——B点位置的近端耦合信号传递到B点需要时间，它们之间的时间差是Tr。

2, 向左找到C点位置：静态线C点位置最开始产生耦合信号是在(1/2)*Tr前，即C点位置(1/2)*Tr前产生的耦合信号目前已经向左传输了(1/2)*Tr时间，此时刚好传输到达了A点位置；所以静态线C点左侧的耦合信号能叠加到A点，而C点右侧的耦合信号都不能叠加到A点的耦合噪声；

——得到结论：A点最大叠加的耦合信号的总能量是：A~C这段距离（(1/2)*Tr*v）产生的耦合信号。

3, 总结：近端耦合信号在A点位置达到最大，而且其值固定不变，所以近端耦合信号最大能叠加传输线距离是：(1/2)*Tr*v（一半上升边沿距离）。

——A点左侧位置的耦合信号幅值呢？当然不能为0，因为近端耦合信号还将源源不断的从右往左叠加过来，其近端耦合信号幅值与A点位置相同。

2，感性耦合

两条传输线之间的感性耦合是指：动态线回路电感与静态线回路电感之间的相互作用。传输线上分布电感看成一连串小变压器在两条线路之间，动态线上受dI/dt的驱动，在静态线上产生一个电压，形成感性耦合电流。

参照容性耦合瞬时耦合电流分析，如下图所示在动态线上传输一个高电平（上升边沿）信号，动态线与静态线之间的共模电感L12，那么在静态线上产生瞬时电压：V12 = L12*ΔV/Tr = Lm* ν *Tr *ΔV/Tr = Lm *ν* I。

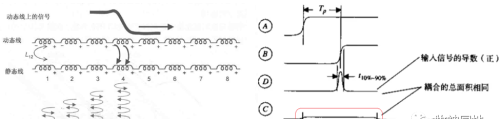
感性耦合与容性耦合产生耦合电压传输模型非常相似，远端和近端耦合电压叠加模式是一样的；不同的是，变压器在静态线上感应出的远端和近端传输的电压脉冲极性相反：

——我们将感性耦合看成是一个变压器，那么变压器有什么特点呢？大家开动脑筋好好回忆下，变压器最大的特点是：匝数比 = 电压比。当然传输线A与B是无法用变压器的匝数比来搞，但是这里明确了一个关系，感性耦合导致的是电压，而非容性耦合的电流。所以就变得简单起来了，感性耦合位置的左右两端就看成是一个电压源，举个栗子：左负右正，即耦合位置左侧是负电压，右侧是正电压。

1. 正脉冲电压向近端（左边，近端耦合）传输；

2. 负脉冲电压向远端（右边，远端耦合）传输。

2.1远端感性耦合

对于感性耦合电压来说，我们只看到了“变压器”两端的电压是VL，但是并不知道耦合位置左侧和右侧的绝对电压值是多少，但是有一点是确定的，感性耦合产生的电流是连续的：假如从右侧进来1A电流，那就要从左侧出去1A电流（容性耦合是左右两侧同时进来或出去电流）。同容性耦合分析类似，感性耦合电压产生后发现静态线的两端阻抗都是一样的（栗子：50Ω），那电压就对半分吧，所以源端感性耦合电压是总感性耦合电压的一半：V = -1/2*VL =-1/2*L12* I/Tr =-1/2*Lm*Len*I/Tr。

静态线远端感性耦合原理同远端容性耦合电压一样，其传输方向同动态线信号传输方向一致，会相互叠加；表现出脉冲波形：宽度为动态线边沿时间，高度与耦合距离相关。但远端感性耦合电压是负电压，而远端容性耦合正电压，两者会相互叠加抵消，减弱远端耦合电压。

2.2近端感性耦合

近端感性耦合电压同远端感性耦合电压值相等，但近端感性耦合电压为正：V = (1/2)*V12 = (1/2)*C*ΔI/Tr = (1/2)*Lm*Len*I/Tr；当耦合长度大于饱和长度，耦合电压将达到一个稳定值：V = (1/2)*1/2*Lm*v*rt*V/rt = (1/4)*Lm*ν *V。同近端容性耦合电流一样，也有如下两个特性：

1. 当耦合长度小于饱和长度，电压峰值小于饱和串扰值，实际耦合电压值与耦合长度和饱和长度比值成正比；

2. 近端串扰时序总时间长度时2*Td，若耦合区域时延为1ns，那么近端噪声持续时间为2ns。

3，串扰和回流

所有的串扰就只有如上两种：1，信号路径之间的容性串扰；2，回路电感之间的感性串扰。那除了这两种之外（忽略阻性串扰），是否还存在其它串扰的可能呢？有爱思考的同学就会想一种情况：如果两条传输线A和B的回流路径重叠，是否会有串扰呢？如下图所示。

1. 传输线A在传输信号时，回流路径上有同样的电流流过；此时信号路径A和信号路径B之间并无容性耦合；而回路路径A和回流路径B之间是同一导体，所以也无容性耦合；

2. 传输线A形成的回路电感与传输线B形成的回路电感，它们之间由于间距很小，是有可能会有较大的感性串扰从传输线A干扰到传输线B的；串扰的大小取决于在回流路径上的趋肤深度，如果趋肤深度小于回流路径铜皮的厚度，回流路径铜皮将起到较好的屏蔽效果，感性串扰就较小（具体后续《电磁兼容基础》中详细分析）；

3. 是否存在回流路径A产生电流影响到回流路径B呢？据我所知是不会的，如果相邻信号层之间走线相互垂直，那么就不会有任何串扰。