土方调配方法有哪些(土方调配方法土木工程)

土方调配方法

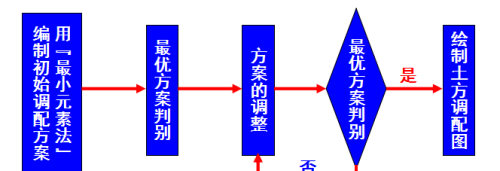
土方调配的步骤：划分调配区（绘出零线）→ 计算调配区之间的平均运距（即挖方区至填方区土方重心的距离）→ 确定初始调配方案→ 优化方案判别→ 绘制土方调配图表。

土方调配的原则：土方调配是土方规划中的一个重要内容。其原则是：力求挖填平衡、运距最短、费用最省，考虑土方的利用，以减少土方的重复挖填和运输。

最优调配方案的确定：最优调配方案的确定，是以线性规划为理论基础，常用“表上作业法”求解。调配的步骤如下：

初始调配方案：下图为一矩形广场，图中小方格内的数字为各调配区的土方量，箭杆上的数字则为各调配区之间的平均运距。试求土方调配最优方案。

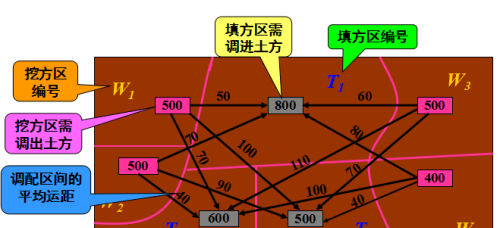
各调配区土方量及平均运距：

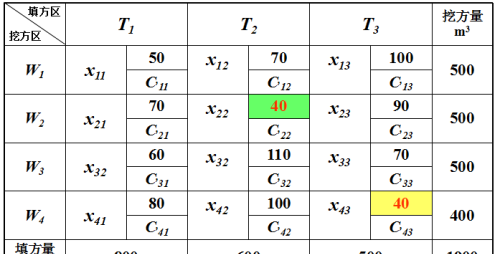
步骤1：选取平均运距最小(C22=C43=40)的方格，确定它所对应的调配土方数，并使其尽可能大。本例选取C43=40，X43=400(W4的全部挖方调往T3)，X41、X42=0 (W4的挖方不调往T1、T2)，在X41、X42的方格内画上“×”

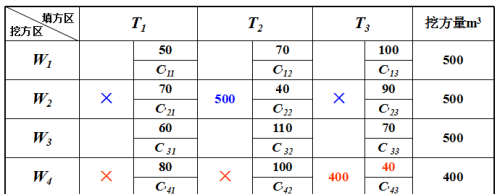
步骤2：重复步骤1，按平均运距由小到大依次计算X22、X11、X31 （C22→C11→C31） ，我们就得到了土方调配的初始方案。

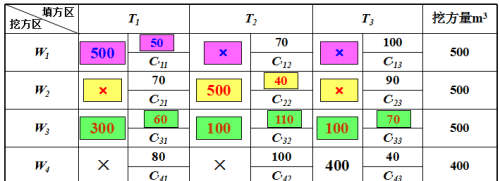
最优方案判别：初始调配方案是按“就近调配”求得的，它保证了挖填平衡、总运输量是较小的，但不一定是最小的，因此还需进行判别。在“表上作业法”中判别最优方案的方法有很多，这里我们介绍引入“假想价格系数”求检验数λij来判别。首先求出表中各方格的假想价格系数，有调配土方的假想价格系数C，ij=Cij ，无调配土方的假想价格系数按下式计算：

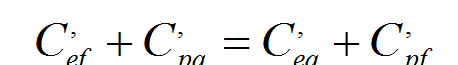
该公式的意义即：构成任一矩形的四个方格内对角线上的假想价格系数之和相等。利用已知的假想价格系数，我们可以逐个求解未知的C，ij。步骤1：在有调配土方的方格内， C，ij=Cij ，将数据填入表中；

步骤2：按任一矩形的四个方格内对角线上的C，ij之和相等，逐个求解未知的C，ij；如：

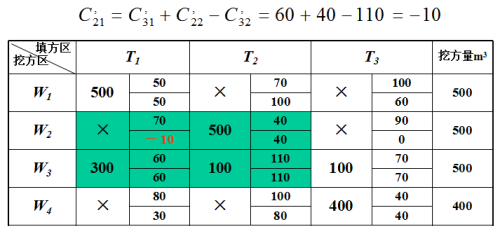
步骤3：引入检验数λ，按下式求出表中无调配土方方格的检验数（即方格右边两小格数字上下相减，将正负号填入表中）：λ12 出现负数说明方案不是最佳方案，需要进行调整。

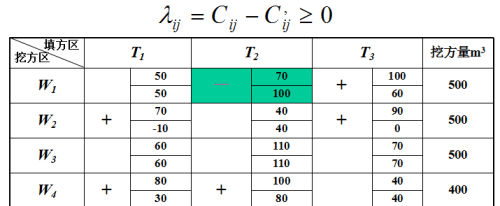
方案的调整：步骤1：在所有负检验数中挑选一个(一般选最小的)，本例即λ12，将它对应的变量 x12 作为调整对象。步骤2：找出x12的闭回路。其作法是，从x12方格出发，沿水平或竖直方向前进，遇到有数字的方格作900转弯(也可不转弯)，如果路线恰当，有限步后便能回到出发点。形成一条以有数字的方格为转角点、用水平或竖直线联起来的闭回路。见下表：

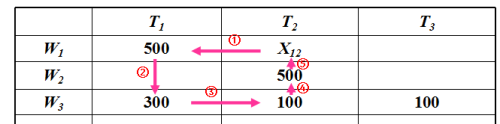
步骤3：从空格 X12出发，沿闭回路（方向任意）行进，在各奇数转角点的数字中挑出一个最小的（本例即X32=100）将它由 X32调到 X12方格中。

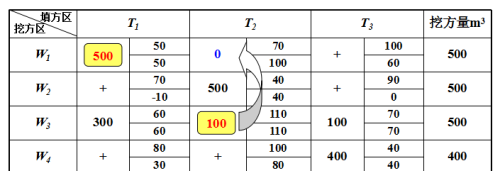
步骤4：将“100”数字填入X12方格中，被调出的X32为0，同时将闭回路上其它奇数次转角（X11）方格内的数字都减去100，偶数次转角（X31）方格内的数字都增加100，使得填、挖方区的土方量仍然保持平衡。这样我们就得到了下表中的新调配方案。

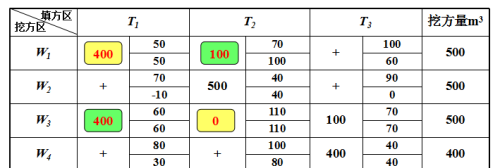
步骤5：对新调配方案按“ ⑵最优方案判别”的方法和步骤再进行判别和检验，如仍出现负数，则重复步骤1～4继续调整，如不出现负数，方案即是最优方案。

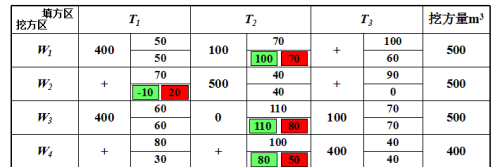
计算无调配土方方格的检验数λ，无负数，方案是最优方案。该优化方案的土方总运输量为：

Z = 400×50＋100×70＋500×40＋400×60＋100×70＋400×40= 94000 （m3·m）

初始方案的土方总运输量为：

Z = 500×50＋500×40＋300×60＋100×110＋100×70＋400×40= 97000（m3·m）

调整后的总运输量减少了3000（m3·m）。

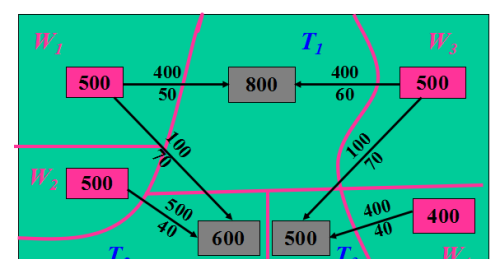
绘出最终土方调配图

温馨提示：通过以上关于土方调配方法内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。