华师版七年级上册整式的加减教案(七上数学第二章2.2整式的加减练习)

华师大版七年级第三章整式的加减，知识点讲解加经典例题分析

1.代数式

由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子，或含有字母的数学表达式称为代数式．

特别注意：(1)不包括等于号（=、≡），不等号（≠、≤、≥、<、>、≮、≯），约等号≈； (2)可以有绝对值，例如：|x|，|−2.25|等。

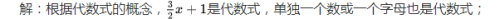
2.代数式书写格式：

(1)两字母相乘、数字与字母相乘、字母与括号相乘以及括号与括号相乘时，乘号都可以省略不写，如：&34;可以写成&34;；&34;应写成&34;，&34;应写成&34;。

(2)字母与数字相乘或数字与括号相乘时，乘号可省略不写，但数字必须写在前面，例如&34;要写成&34;，不能写成&34;；&34;要写成&34;，不能写成&34;。

(3)代数式中不能出现除号，相除关系要写成分数的形式。

(4)数字与数字相乘时，乘号(也可以写作 · )仍应保留不能省略，或直接计算出结果.例如&34;不能写成&34;，最好写成&34;。

指点迷津：相乘时，只有数字与数字相乘时乘号不可省略，其他情况全部省略，书写顺序应为先数字，后字母（按照字母表顺序书写），最后括号。自己书写时不要使用 · 代替乘号，要直接省略。

3.列代数式

把问题中与数量有关的词语，用含有数、字母和运算符号的式子表示出来的过程。

4.代数式求值

用数值代替代数式中的每个字母，然后计算求得结果的过程。

对于特殊的代数式也可采取如下方法来解：

①给出代数式中的所有字母的值，一般要先化简代数式，然后再代入求值；

②给出代数式中所含字母之间的关系，一般把所要求的代数式通过恒等变换，转化成为用已知关系表示的形式，再整体代入求值；

③在给定条件中，字母之间的关系不明显，字母的值隐含在题设条件中，一般应先由题设条件求出字母的值，再代入求代数式的值。

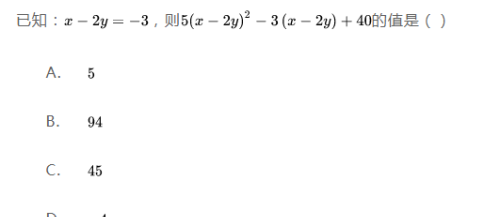
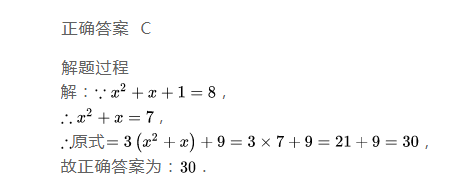
5.单项式

形如−x,12m2,3xy,2πd,都是数或字母的乘积，这样的式子叫做单项式。特别地，单独的一个数或一个字母也是单项式。

特别注意：单项式是一个乘积的形式，不能出现加号与减号。

6. 单项式的系数

单项式中的数字因数叫做这个单项式的系数（可以简单理解为字母前边的数字和符号就是系数）。

7. 单项式的次数

一个单项式中，所有字母的指数的和叫做这个单项式的次数。

附：代数式的定义：用运算符号（加、减、乘、除、乘方、开方）把数或表示数的字母连接而成的式子，单独的一个数或一个字母也是代数式。

指点迷津：单项式的系数就是看字母前边的数字与符号，而单项式的次数则是看字母，需要把所有字母的指数相加作为次数，特别注意，π是一个数字，不是字母。

8.多项式

由若干个单项式相加组成的代数式叫做多项式。

9.多项式的项与项数

多项式中每个单项式叫做多项式的项，有几个单项式组成项数就是几。

10.多项式的次数

多项式中这些单项式的最高次数，就是这个多项式的次数。

求法：①先求出多项式每一项的次数；②取最高次数作为多项式的次数。

附：代数式的定义：用运算符号（加、减、乘、除、乘方、开方）把数或表示数的字母连接而成的式子，单独的一个数或一个字母也是代数式。

11.降幂排列与升幂排列

降幂排列：把一个多项式各项的位置按照其中某一个字母的指数从大到小的顺序排列起来，叫做这个多项式按这个字母的降幂排列。

升幂排列：把一个多项式各项的位置按照其中某一字母的指数从小到大的顺序排列起来，叫做这个多项式按这个字母的升幂排列。

特别注意：降幂排列与升幂排列时要注意三点①看清按哪个字母排列；②看清是升幂还是降幂；③各项移动时，要连同它的符号一起移动。

12.整式

单项式与多项式统称为整式。

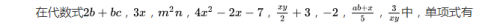
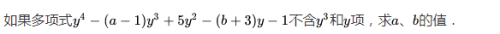
13.同类项

所含字母相同，并且相同字母的指数也相同的项叫做同类项。几个常数项也是同类项。

特别注意：同类项是针对单项式而言的，不能说几个多项式是同类项。

14.合并同类项

把多项式中的同类项合并为一项，叫做合并同类项．

法则：同类项的系数相加，所得结果作为所得项的系数，字母连同它的指数不变。

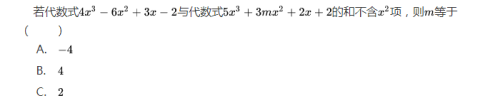
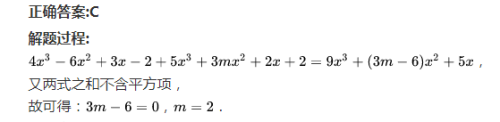
15.去括号与添括号

（1）去括号法则

括号前面是&34;，把括号和它前面的&34;去掉，括号内各项都不改变符号；

括号前面是&34;，把括号和它前面的&34;去掉，括号内各项都改变符号。

例如：+(a+b−c)=a+b−c；−(a+b−c)=−a−b+c。

（2）添括号法则

所添括号前面是&34;，括到括号里的各项都不改变符号；

所添括号前面是&34;，括到括号里的各项都要改变符号。

例如：a+b−c=+(a+b−c)；−a−b+c=−(a+b−c)。

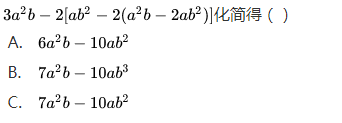
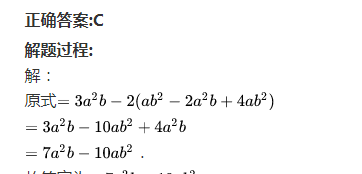
16.整式的加减

整式的加减满足去括号与添括号、乘法分配律和合并同类项的运算规律。

指点迷津：整式的加减就是先进行去括号，再进行合并同类项即可。

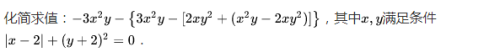
温馨提示：通过以上关于华师大版七年级第三章整式的加减，知识点讲解加经典例题分析内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。