从理论到实践，奈奎斯特采样定理，我终于闹明白了

本文讨论采样定理，解释其在实际混合信号系统中的重要性。今天，我们需要考虑这个定理在指导以设计功能电路和系统为目标的电气工程师的决策中的作用。

香农采样定理的阐述如下：

如果一个系统以超过信号最高频率至少两倍的速率对模拟信号进行均匀采样，那么原始模拟信号就能从采样产生的离散值中完全恢复。

用理论指导践，但并没有具体的说明。换句话说，香农定理并没有告诉我们如何设计一个采样系统；相反，它只帮助我们去理解采样系统，并提供了一个指导和支持工程师工作的框架。因此，了解理论和实践的差异是很重要的，在采样理论中，也许最重要的差异就是所需的采样率。

采样和混叠

当采样频率（fS）小于最大信号频率（fMAX）的两倍时，就会引起混叠，从而使子频谱重叠。

我认为，大多数人们都会自然地将“混叠”一词理解为固有的消极的含义，这是一个必须避免的潜在问题。然而，广义上的混叠是将信号从连续波形转换为离散值序列的一个组成部分。

我一直使用“子频谱”这个词来指代采样产生的频谱副本，但更加正式的名称应该是混叠。

我们创造混叠，原始信号频率“伪装”成不同的频率——每次我们进行模数转换时，无论采样率如何。当采样数据从数字转换回模拟时，这些混叠便成为了模拟信号的一部分，因此D/A转换产生的模拟信号与采样信号不同。所以，如果我们想要完美地重构原始模拟信号，就必须消除混叠的影响。

正如我们所知道的，为了防止由混叠引起的信号被破坏，我们需要以奈奎斯特速率或更高的速率进行采样。如果我们不遵守这个基本要求，那么就无法消除混叠——尽管我们可以一目了然地看到采样数据，但混叠已经永久地与原始频谱混合在一起了，我们无法将其区分开来。

但是，信号重构只能从足够的采样频率开始。而第二个基本要求，则是低通滤波。

滤波重建

如果我们以高于奈奎斯特速率进行采样，则仍然会有混叠，但现在真实频谱与混叠频谱之间存在着差距：

这使得我们可以通过将数字化波形转换为模拟波形，然后使用低通滤波器来恢复原始信号：

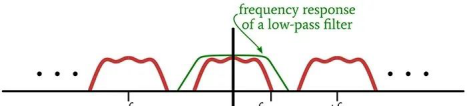
用来消除（或者更确切地说是减轻）重构模拟信号中混叠影响的低通滤波器，称之为重建滤波器。这是在D/A转换后应用的模拟滤波器。这里，我用斜体字强调两点：

第一，我们不能通过数字滤波来消除混叠。混叠是采样的量化数据的固有属性，因此无法在数字领域中消除（尽管过采样和插值可以降低模拟滤波的要求）。

第二，重建滤波器是用来消除混叠的，但它不是抗混叠滤波器！“抗混叠滤波器”指的是在A/D转换之前应用的低通滤波器。

理想滤波器vs真实滤波器

如果你仔细思考一下前面的图表，你可能会开始理解为什么香农定理不是设计混合信号电子系统的“操作”指南了。如果我们将采样率降低到理论极限，那么傅立叶变换看起来就是这样的：

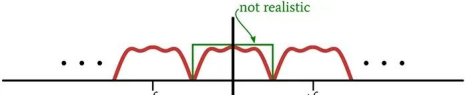
在理想的数学领域，我们仍然可以区分真实频谱与混叠频谱。然而，物理分量不能创造具有“砖墙”类型的频率响应，而是需要垂直向下切分，从而完美地过滤掉不需要的频率内容：

此外，我们通常更倾向于避免使用接近“砖墙”响应的过滤器所需的成本、复杂性和板空间。取而代之的是，我们使用过采样。

通过以远高于奈奎斯特速率的速率对信号进行采样，我们可以确保真实频谱与最近的混叠之间存在较大的频率间隔。这个较大的间隔使得我们更容易构建有效的重建滤波器，因为幅度响应会缓慢下降，并且仍然会在混叠频谱上产生明显的衰减。通过大量的过采样，即使是一阶RC低通滤波器也可以提供足够的混叠抑制。

在指定的应用程序中，需要多少过采样并没有固定的规则，但我喜欢采样率至少是最高信号频率的五倍。如果你的信号频率接近ADC的最大采样率，那么你可能需要更接近奈奎斯特速率才行，然后投入更多的时间和金钱在你的重建滤波器上。

结 语

通过本文我们看到，香农采样定理需要适应实际电路设计的约束，尽管当采样率等于最高信号频率的两倍时，完美重构在数学上是可能实现的，但这种方法需要理想化的低通滤波器，因此不能直接适用于工程系统。

至于我提到的另一个重要问题，重建滤波器与抗混叠滤波器之间的区别，我们将在下一篇文章中进行讨论。

最后，需要说明一下，由于个人能力有限，有些词句可能翻译得比较生硬，建议有英文阅读能力的小伙伴儿一定要去阅读原文。另外，文中翻译如有不当之处，还请批评指正。