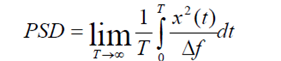随机振动之频谱分析和傅里叶变换

通常，对于正弦振动，理解相对比较简单，波形也很好理解，如下图。

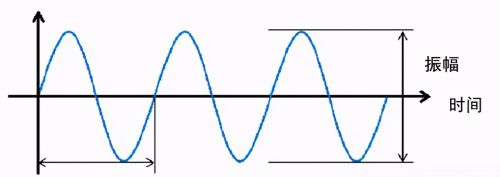
其实，在实际的振动过程中，正弦振动少之又少。比如，按照正弦振动条件实施产品的易损性评价后，结果还是不能得到正确的结果。因为在实际振动中，包含了带有不同频率和振幅的正弦振动，我们把这种由不同频率和不同幅值组成的波形称为随机波，对应的振动称之为随机振动。如果利用随机振动进行可靠性试验和环境试验，得到的结果肯定能高很多。

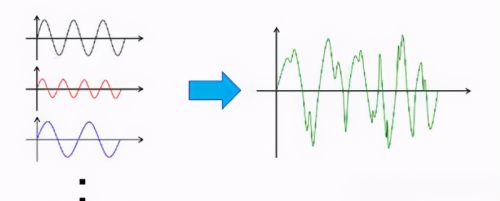
读到上面文字后，不禁会问，随机振动是由各种各样不同频率和幅值的正弦振动组合而成，各种成份的正弦振动是如何分配？这是怎么分析得到的呢？确实是这样的吗？

将时间域内含有的变化信息置换到频率域的分析方法，即频谱分析。捕捉到随机振动中对应时间变换的信息（波形），应用频谱分析和傅里叶变换，即可解决上面的问题。

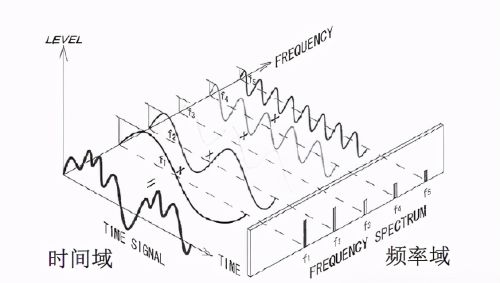
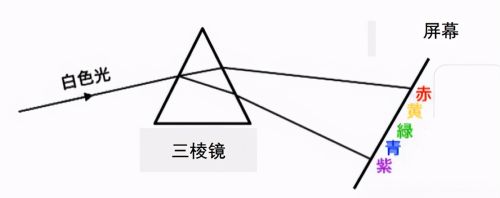
频谱分析和傅里叶变换理解上有一定的难度，可以用自然界的白色光来加以理解。白色光是由各种波长的光混合而成，或者反过来说，各种波长的光组成白色光，通过三棱镜即可实现，如下图。其实不只是含有5种颜色的光，利用特殊仪器对屏幕上的光进行检测，可以得到一个连续的光谱图，得到白色光中各波长成份的强度分布情况。

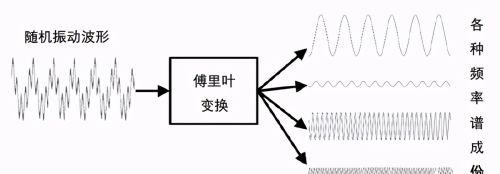
将三棱镜更换为傅里叶变换，便可很好的理解随机振动的频谱分析。通过傅里叶变换即可得到随机振动波形中各个频率对应的幅值和相位，反过来就是逆傅里叶变换。

公式，

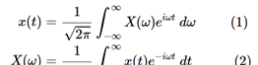
X(ω)是x(t)的傅里叶变换， x(t)是X(ω)的逆傅里叶变换，X(ω)即各个频率对应的幅值，|X(ω)|2是各个频率对应的能量。

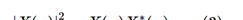
X＊(ω)是X(ω)的共轭复数X＊(ω)= X(-ω)，即，并定义能量|X(ω)|2与ω的分布关系为功率谱。式(2)中，如果x(t)只存在区间[-T/2，T/2]，那么X(ω)是有限的，便可得到功率谱。但是，若x(t)存在于无限空间，X(ω)也是无限的，得不到功率谱，那该如何是好？于是便提出了功率谱密度P(ω)（PSD：Power Spectral Density）的概念，即单位时间内的能量分布情况。

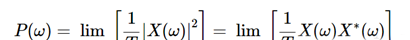
上式中，对功率谱取时间平均，平均时间取无穷大的极限。但在实际中基本上不用上式求PSD，而是利用自相关函数和功率谱密度的关系，再使用傅里叶变换和维纳-辛钦公式求得。

随机振动信号是时域无限信号，不具备可积分条件，因此不能直接进行傅里叶变换。一般用具有统计特性的功率谱来作为谱分析的依据，功率谱和自相关函数是一对傅里叶变换。功率谱具有单位频率的平均功率量纲，标准叫法应该是功率谱密度，通过它可以看出随机振动信号的能量随频率的分布情况。比如白噪音，就是一条平直线。

一般随机振动试验中的功率谱密度是针对平稳随机过程的，其样本函数一般不是绝对可积的，因此不能直接用傅里叶变换，可以有三种办法来重新定义谱密度，克服困难。一是用相关函数的傅里叶变换来定义谱密度；二是用随机过程的有限时间傅里叶变换来定义谱密度；三是用平稳随机过程的谱分解来定义谱密度。求取PSD是个很复杂的过程，还好现在技术的进步，我们只需要理解概念，懂得仪器的操作便能求取，初学者只需要记住和理解下面这些内容即可。

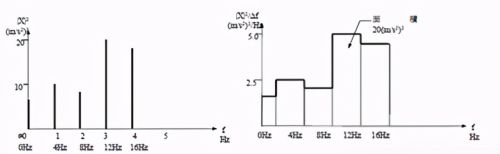
功率谱密度是随机振动试验中使用的一种谱，用通过在中心频率（Δf）设置的窄幅过滤器的加速度信号平方的平均值的单位频率值表示，单位g2/Hz。也称为加速度谱密度，此时单位（m/s2）2/Hz。