静态时序分析基础

为了确保寄存器在时钟沿稳定采集数据，那么必须要满足寄存器的建立，保持时间要求。

建立时间要求：在寄存器有效时钟沿之前至少Tsetup时间，数据必须到达且稳定。如下图所示。

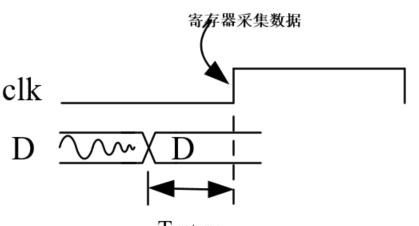
保持时间要求：在数据采集有效时钟沿之后，数据必须维持最短Thold时间不变。如下图所示。

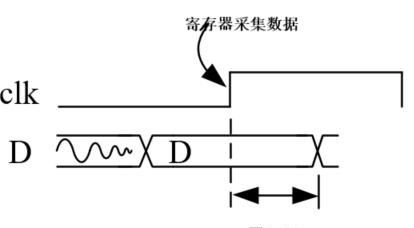
建立时间裕量计算

同步时序电路如下图所示。这里对后面一个寄存器进行建立时间裕量分析。

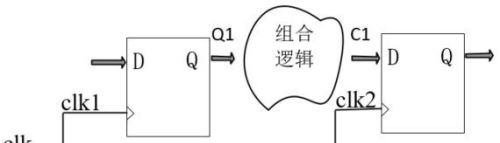
其中寄存器的输出延时为Tcq，即时钟有效沿之后延时Tcq时间，数据才到达寄存器Q端。第一个寄存器有效时钟沿之后Tcq时间，数据才到达Q1端，如下图所示。

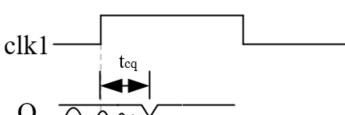
再经过组合逻辑运算，得到数据C1，其中组合逻辑的延时为Tlogic。时序如下图。

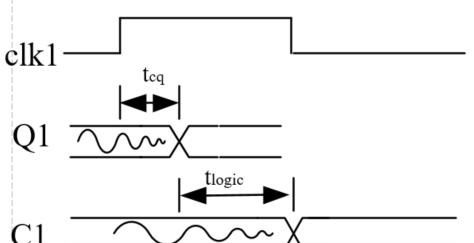
从这里可以看到，如果clk2和clk1之间没有延时。那么对于后面的寄存器而言，数据提前于采样时钟沿之前Tcycle-（Tcq+Tlogic）时间到来，且稳定。其中Tcycle为时钟周期。

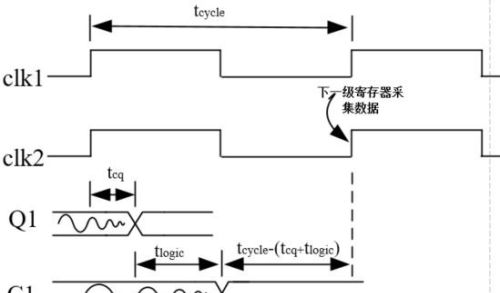
由于寄存器要求的建立时间为Tsetup，故电路必须满足 Tcycle -（Tcq+Tlogic）- Tsetup>0 。建立时间裕量 Tset_slack = Tcycle -（Tcq+Tlogic）- Tsetup

如果clk1与clk2之间存在skew，如下图所示，如正skew。得建立时间裕量为

Tset_slack = Tcycle -（Tcq+Tlogic）- Tsetup + Tskew

这是对建立时间有益的。

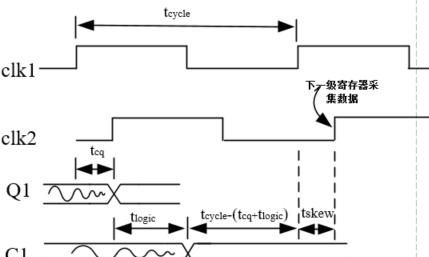
保持时间裕量计算

在时钟没有skew的情况下。在后一个寄存器有效采样时钟沿之后，同时新的C1只有经过Tcq+Tlogic之后才会到达。故要满足保持时间要求，只需要满足Tcq+Tlogic>Thold。保持时间裕量Thold_slack = Tcq+Tlogic-Thold

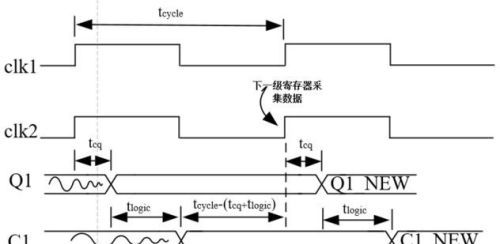
如果clk1与clk2之间存在skew。如下图所示（正skew）。

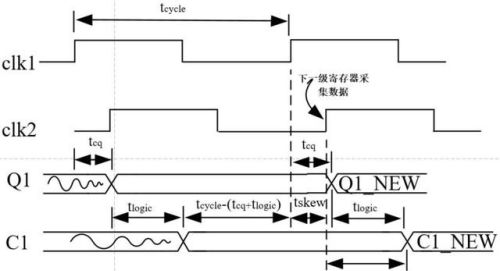
可以看到，C1_NEW在clk2时钟沿后，Tlogic+Tcq-Tskew就改变了。此时保持时间裕量Thold_slack = Tcq+Tlogic-Thold - Tskew 。可以看到，正skew对保持时间是无益的。

总结

可以看到，必须满足建立时间要求和保持时间要求，级满足如下关系式。

Tset_slack = Tcycle -（Tcq+Tlogic）- Tsetup + Tskew>0

Thold_slack = Tcq+Tlogic-Thold - Tskew > 0

从中可以看出，建立时间与保持时间要求是一对矛盾的关系，在设计电路时，我们要折中考虑。