二极管恒压降 压降在电路中计算方法
什么是二极管恒压降
就是正向导通时,不管外电压多大,电流多大,在二极管上的压降维持不变。
在二极管恒压降模型中,只考虑二极管PN结的内建电场的作用, 不把二极管看做有电阻的。这样,二极管正向导通时,压降只与内建电场有关,而内建电场恒定,所以,压降也是恒定的。
二极管的模型有多种:
1.理想模型
所谓理想模型,是指在正向偏置时,其管压降为零,相当于开关的闭合。当反向偏置时,其电流为零,阻抗为无穷,相当于开关的断开。具有这种理想特性的二极管也叫做理想二极管。
在实际电路中,当电源电压远大于二极管的管压降时,利用此模型分析是可行的。
2.恒压降模型
所谓恒压降模型,是指二极管在正向导通时,其管压降为恒定值,且不随电流而变化。硅管的管压降为0.7V,锗管的管压降为0.3V。
只有当二极管的电流Id大于等于1mA时才是正确的。
在实际电路中,此模型的应用非常广泛。
3.折现模型
此时考虑二极管固有的电阻,把二极管看做恒压降模型加上一个串联的定值电阻,在伏安特性曲线上,导通电压与电流成线性关系。
4.交流小信号模型
动态电阻指增量电压下产生的增量电流,它们形成的比值Rac=dU/dI,正是曲线斜率的倒数,在工作点Q的基础上,增加(或减少)一个增量电压:dU,那么电流将沿着曲线上升(或下降)一段:dI。曲线斜率为dI/dU,所以动态电阻为它的倒数。动态电阻当然与正向导通有关,因为曲线斜率在不同的工作点并不相同。
二极管恒压降模型
二极管的恒压降模型在实践中使用是比较广泛的。
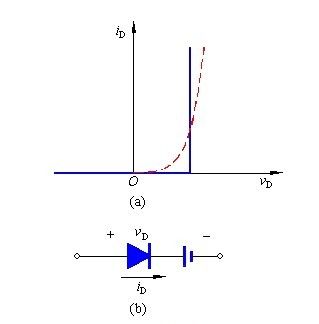
它对二极管伏安特性在一定程度上进行了合理的近似建模。
该模型中,使用一个理想二极管模型和直流电源串联实现。理想二极管的单向导电决定了,恒压降模型也是单向导电。在外加正向电压时,只有大于0.7V(硅管)才会产生正向导通电流。
判断二极管导通状态
如何判断电路中的二极管是否导通,其实靠的是试验法。
先将电路中的二极管拿掉,计算原位置处两端正向电压;如果大于0.7v,那么把二极管再放回原位置的话,二极管必然是导通的。
举例:
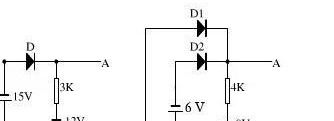
(a)图中,拿掉二极管D可知,D阳极电位为-15v,阴极电位为-12v,D正向电压为-3v,故D不导通,AO两端电压为-12V。
(b)图,同时拿掉D1,D2。
得到D1原位置处两端电压为0-(-9)=9v
得到D2原位置处两端电压为-6-(-9)=3v
两个二极管都导通吗?不一定!由于二极管导通后会导致电路中各点电位重新分配,所以将二极管接回原电路的时候要一个一个来。
D1两端压差有9V,比D2的压差要高。我们就先将D1接回原电路,此时,A点电位是-0.7v,重新计算D2处两端压差为-6-(-0.7)=-5.3v。看到了吧,此时如果将D2接回电路是不导通的。
判断输出电压波形
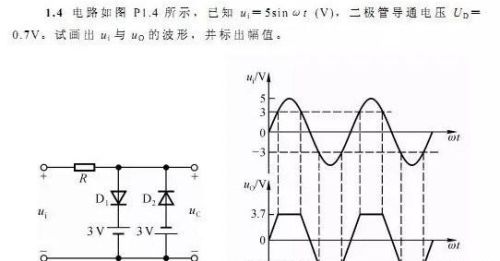
分析如下:
D1在ui大于3.7v时导通,D2截止,此时uo=3.7v。
D2在ui小于-3.7v导通,D1截止,此时uo=-3.7。
D1D2同时导通的情况不存在。
D1D2在-3.7《ui《3.7时,都截止,对输出uo没影响,uo=ui
压降最简单计算公式
一,线路压降计算公式;
△U=2*I*R;
式中 I为线路电流 ,R为电阻,L为线路长度 。
电阻率ρ 1, 铜为0.018欧*㎜2/米 2, 铝为0.028欧*㎜2/米 。
二,电流计算公式,I=P/1.732*U*COS? 。
三,电阻计算公式,R=ρ*l/s(电缆截面mm2) 。
四,电压降△U=IR<5%U就达到要求了。 例:在800米外有30KW负荷,用70㎜2铜芯电缆看是否符合要求?
解; I=P/1.732*U*COS?=30/1.732*0.38*0.8=56.98A 。
R=Ρl/电缆截面=0.018*800/70=0.206欧姆。
△U=2*IR=2*56.98*0.206=23.44》19V (5%U=0.05*380=19) 不符合要求。
套公式用95MM2的铜芯电缆。
2、单相电源为零、火线(2根线)才能构成电压差,三相电源是以线电压为标的,所以也为2根线。电压降可以是单根电线导体的损耗,但以前端线电压380V(线与线电压为2根线)为例,末端的电压是以前端线与线电压减末端线与线(2根线)电压降,所以,不论单相或三相,电压降计算均为2根线的
就是欧姆定律:U=R*I 但必须要有负载电流数据、导线电阻值才能运算。铜线电阻率:ρ=0.0182,铝线电阻率:ρ=0.0283
例: 单相供电线路长度为100米,采用铜芯10平方电线负载功率10KW,电流约46A,求末端电压降。
解;1, 求单根线阻: R=ρ×L/S=0.0182×100/10≈0.18(Ω)。
2, 求单根线末端电压降: U=RI=0.17×46≈7.8(V) 。
3, 单相供电为零、火2根导线,末端总电压降: 7.8×2=15.6(V)。