阿基米德折弦定理推论(阿基米德折弦定理证明办法方法)

初中数学：阿基米德折弦定理

ııllı 不去做，就只能停留在现在ııllı●━━━━━━─────── ⇆ ◁ ❚❚ ▷ ↻

作者：究竟数学

我只能带你到这扇门了，

后面你必须得自己走过去。

讲义阿基米德折弦定理：一个圆中一条由两长度不同的弦组成的折弦所对的两段弧的中点在较长弦上的射影，就是折弦的中点。

AB和BC组成圆的折弦，BC>AB，M是弧ABC的中点，MD⊥BC，垂点为D。则CD=AB+BD。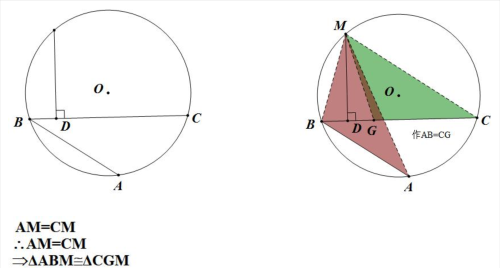

例题

典例1. 如图，已知等边三角形ABC内接于圆0,AB=2,点D为弧AC上一点，ABD=45°,AEBD于E，求BDC的周长。

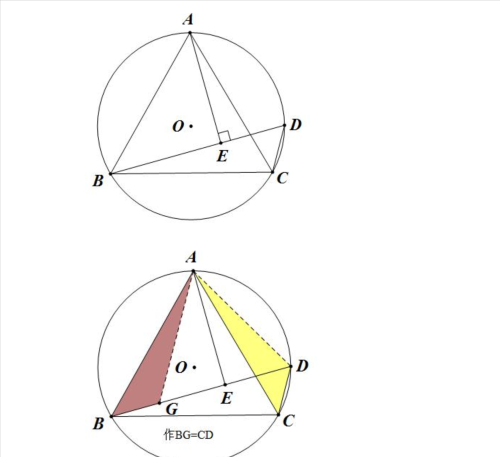
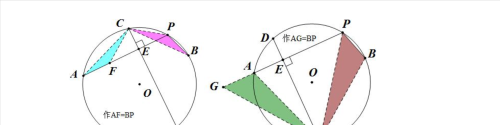
典例2. 已知：如图1，在圆o中，C是劣弧AB的中点，直线CDAB于E，易证得：AE=BE，从圆上任意一点出发的两条弦所组成的折线，成为该圆的一条折弦。如图2，PA、PB组成圆o的一条折弦，C是劣弧AB的中点，直线CDPA于E,

（1)求证：AE=PE+PB

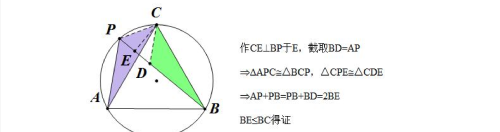
典例3. 如图，ABC内接于圆0，AC>BC，点D为弧ACB的中点，求证：=AC·BC+.

已知圆O是等边ABC的外接圆，P是圆O上一点，求证PA+PBAC+BC.

温馨提示：通过以上关于初中数学：阿基米德折弦定理内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。