挠度计算的主要原理(挠度计算公式一览表)

挠度是什么，实际工程中挠度计算实例

搞工程的，想必对挠度都不陌生，何为挠度？挠度，指的是比较长的杆件在一定载荷作用下，横截面相对于理论位置的偏移量。如下图，长杆件两端铰接，在均布载荷q的作用下，长杆会自然产生下垂，不难推断出中间位置的下垂量最大，称之为最大挠度。

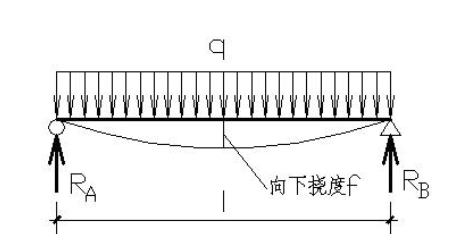
何为挠度

在工程领域，对于一些重要关键位置必须要做挠度校核。例如，修建桥梁，需要对桥面挠度校核，挠度过大会存在安全隐患；在精密加工机床上，必须对主轴挠度校核，挠度过大会影响加工精度；在钢梁结构中，必须对关键钢梁挠度校核，挠度过大会造成钢梁损坏断裂。

简化模型过程中，一定要分清楚，梁的连接位置是固定连接还是支撑连接，不同的连接方式对计算结果产生很大的影响。笔者分享几个非常典型常用的挠度计算公式，建议收藏。

公式一：

杆件受均布载荷，q N/mm, 杆件长度Lmm, 杆件弹性模量E, 杆件截面惯性矩I，最大挠度变形量fmax

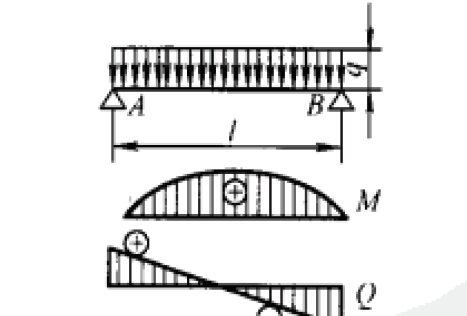
两端支撑，受均布载荷

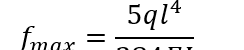
公式二：

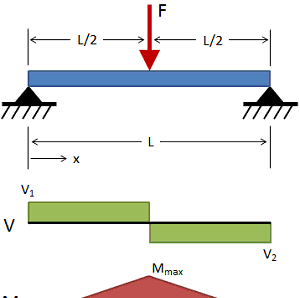
两端铰接，梁中点受载荷P

杆件载荷P N/mm, 杆件长度Lmm, 杆件弹性模量E, 杆件截面惯性矩I，最大挠度变形量fmax

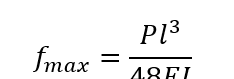
公式三：

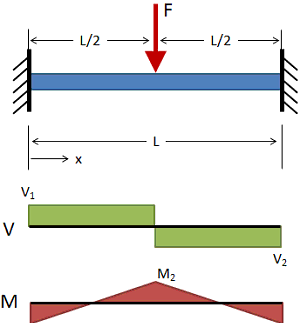
两端固定，梁中间受载荷P

杆件载荷P, 杆件长度L, 杆件弹性模量E, 杆件截面惯性矩I，最大挠度变形量fmax

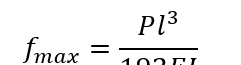
公式四：

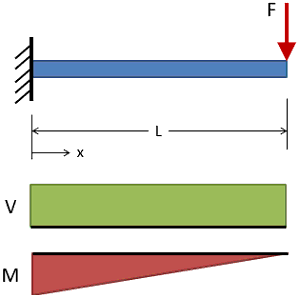
一端固定悬臂梁

杆件载荷P, 杆件长度L, 杆件弹性模量E, 杆件截面惯性矩I，最大挠度变形量fmax

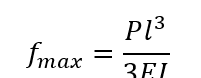
公式五：

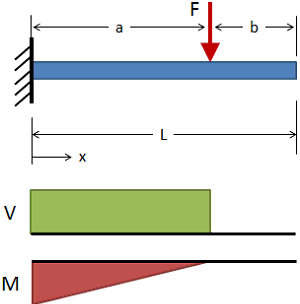
一端固定悬臂梁

杆件载荷P且受力位置在距离固定点a处, 杆件长度L, 杆件弹性模量E, 杆件截面惯性矩I，最大挠度变形量fmax

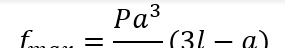
工程实际应用：

假设有一根工字型钢梁25a，长度4000mm，两端简单支撑，钢梁上承受7吨的载荷，为简化模型，认为是均布载荷。请校核钢梁的最大挠度变形。

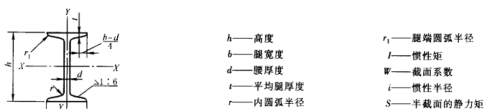
工字钢

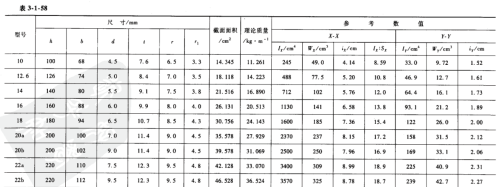
25a相关参数

已知：

25a工字钢，查机械手册知截面惯性矩I=5020cm^4=5020x10^4 mm^4

一般钢材弹性模量E=210000N/mm^2，或者210Gpa

实际应用中会见到不同的单位，例如压强的单位帕斯卡，即Pa.

1Gpa=1000Mpa ，1Mpa=1000 000 Pa ，1Pa=1N/m²

因此，1Gpa=1000 000 000N/m²=1000 N/mm2

钢梁均布载荷q=70000N/4000mm=17.5N/mm

计算过程：

计算过程

注意：实际计算中要注意单位换算，单位要分子分母相同，最后都可以抵消掉。E是材料的弹性模量，是材料的固有特性，只与材料有关。比如一般钢材的弹性模量210Gpa，一般铝型材弹性模量70Gpa左右。I截面惯性矩只和受力材料截面形状、弯曲方向有关，对于常用的方管、型钢，都可以在机械设计手册中查到相关参数，对于一些圆柱形，矩形等常规截面，有一定的公式可以计算截面惯性矩，由于篇幅限制，这里就不在一一展开。

从计算过程可以得知，钢梁中间位置最大挠度变形量55mm左右，这个变形量还是稍微有点大的。建议增大所选钢梁或增加固定支撑点。

温馨提示：通过以上关于挠度是什么，实际工程中挠度计算实例内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。