初中二次函数(初中数学,二次函数)

初中数学中考知识点复习函数篇之二次函数

二次函数是初中阶段函数最难的一部分，也是中考考核的重点。需要好好学习二次函数的定义、性质及应用。

二次函数的定义：一般地,形如y=ax²+bx+c(a、b、c为常数,a≠0)的函数,叫做二次函数.其中,x是自量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.

注意:

(1)等号左边是函数y，右边是关于自变量x的整式

(2) a,b,c为常数，且a≠0.

(3)等式右边的最高次数为2，可以没有一次项和常数项，但不能没有二次项

(4) 自变量x的取值范围是任意实数，但是当自变量表示实际意义时，自变量的取值范围就不一定是全体实数。

判断一个函数是不是二次函数，要抓住二次函数的结构特征：（1）解析式是关于自变量的整式；（2）自变量的最高次数是2；（3）化简后二次项系数不为0. 除此之外，二次函数除有一般形式y=ax²+bx+c(a≠0)外，还有其特殊形式,如y=ax²、y=ax²+c等.

二次函数的一般式与前面我们学过的一元二次方程的联系和区别：右边是一样的，二次函数的y=0就是一元二次方程，区别在于一个是函数，一个是方程。

二次项系数a的绝对值大小与开口大小的关系，当a的绝对值越大，开口越小。

求不规则图形的面积，常采用等面积割补法，将不规则图形转化为规则图形以方便求解。

二次函数y=ax²+bx+c的顶点式

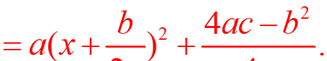
这个结果通常称为顶点坐标公式，最好是会推理。

因此,二次函数y=ax²+bx+c的图象是一条抛物线

二次函数二次函数y=ax²+bx+c的图象和性质

二次函数图像的性质

确定二次函数的关系式y=ax²+bx+c (a,b,c为常数,a ≠0)，通常需要3个条件; 当知道顶点坐标（h,k）和图象上的另一点坐标两个条件时，用顶点式y=a(x－h)2+k可以确定二次函数的关系式。

在什么情况下，一个二次函数只知道其中两点就可以确定它的表达式？

1.用顶点式y=a(x－h)2+k时，知道顶点（h,k）和图象上的另一点坐标,就可以确定这个二次函数的表达式。

2. 用一般式y=ax²+bx+c确定二次函数时，如果系数a,b,c中有两个是未知的，知道图象上两个点的坐标，也可以确定这个二次函数的关系式.

待定系数法求解二次函数的过程：

(1)设二次函数的表达式；

(2)根据图象或已知条件列方程(或方程组)；

(3)解方程（或方程组）,求出待定系数；

(4)答：写出二次函数的表达式.

一元二次函数的应用：“最大面积” 问题解决的基本思路

1. 阅读题目，理解问题

2.分析问题中的变量和常量,以及它们之间的关系.

3.用数量的关系式表示出它们之间的关系.

4.根据二次函数的最值问题求出最大值、最小值

5.检验结果的合理性

二次函数的图像与x轴交点的个数由b2-4ac决定，当Δ＞0时，与x轴有两个交点，当Δ=0时，与x轴有一个交点，当Δ＜0时，与x轴没有交点.

二次函数的图像与x轴交点的横坐标就是一元二次方程的根。

一元二次与二次函数性质

需要灵活运用一元二次函数图像的对称性，关于对称轴对称的两个点的纵坐标相同，横坐标到对称轴的距离相同。

需要特别注意当常数项和一次项的为0的情况，这种是一种特殊的一元二次函数。

温馨提示：通过以上关于初中数学中考知识点复习函数篇之二次函数内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。