长方体和正方体的思维导图(长方体和正方体的表面积)

长方体和正方体

一、认识长方体和正方体的特征及它们的展开图。

1.长方体是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形。在一个长方体中,相对的面完全相同,相对的棱长度相等。长方体有8个顶点,12条棱。

2.相交于同一个顶点的三条棱的长度分别叫做长方体的长、宽、高。

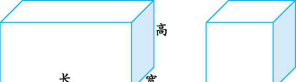
3.长方体12条棱的长度和叫做长方体的棱长总和。

长方体的棱长总和=4条长+4条宽+4条高=(长+宽+高)×4。

用字母表示:C=(a+b+h)×4。

4.正方体是由6个完全相同的正方形围成的立体图形,正方体有8个顶点,12条棱,12条棱的长度都相等。

5.正方体是长、宽、高都相等的长方体,正方体是特殊的长方体。

6.正方体的棱长总和=棱长×12。用字母表示:C=12a。

7.认识长方体和正方体的展开图。

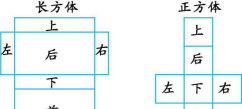
二、掌握长方体和正方体表面积的计算方法,并能运用所学知识解决一些简单的实际问题。

1.长方体或正方体6个面的总面积,叫做它的表面积。

2.长方体的表面积=(长×宽+长×高+宽×高)×2。

用字母表示:S=(ab+ah+bh)×2。

3.正方体的表面积=棱长×棱长×6。

用字母表示:S=6a2。

4.如果把一个长方体沿一个面截成n块,就增加了2(n-1)个截面,每个截面的4条棱就是增加的棱,总共增加了8(n-1)条棱。

三、了解体积的意义及计量单位,会进行单位之间的换算。

1.物体所占空间的大小叫做物体的体积。

2.常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm3、dm3、m3。

3.棱长是1 cm的正方体,体积是1 c;

棱长是1 dm的正方体,体积是1 dm3;

棱长是1 m的正方体,体积是1 m3。

四、掌握长方体和正方体体积的计算,并会运用公式解决实际问题。

1.长方体的体积=长×宽×高。

用字母表示:V=abh。

2.正方体的体积=棱长×棱长×棱长。

用字母表示:V=a3。

3.长方体和正方体体积的统一公式:

长方体和正方体的体积=底面积×高。

用字母表示:V=Sh。

4.体积单位间的进率:

1立方分米=1000立方厘米　　　1立方米=1000立方分米

相邻的两个体积单位间的进率是1000。

5.体积单位的换算与以前学过的长度、面积单位的换算方法基本相同,只是相邻的两个体积单位间的进率是1000。

6.已知长方体的体积、长、宽、高四个量中的任意三个量,都能求出另一个未知量。

a=V÷b÷h　　b=V÷a÷h　　h=V÷a÷b

五、认识容积的意义及计量单位,会进行容积单位和体积单位的互化。

1.容器所能容纳物体的体积,通常叫做它们的容积。

2.计量容积,一般用体积单位。计量液体的体积,如水、油等,常用容积单位升和毫升,也可以写作L或mL。

3.容积单位的换算:1升=1000毫升

容积单位和体积单位的关系:1升=1立方分米

　　　　　　　　　　　　　 1毫升=1立方厘米

4.长方体或正方体容器容积的计算方法跟体积的计算方法相同,但要从容器里面量长、宽、高。

六、测量不规则物体的体积。

测量不规则物体的体积,通常采用排水法:

1.利用有刻度的量筒或量杯,记录下放入不规则物体前后的刻度,上升的那部分水的体积就是不规则物体的体积。

2.容器内装满水,把不规则物体放进容器里(完全浸没),溢出的水的体积就是不规则物体的体积。

七、把棱长为1厘米的小正方体拼成棱长为n厘米的大正方体后涂色,涂色面的规律是:

1.三面涂色的小正方体的个数=正方体的顶点个数=8;

2.两面涂色的小正方体的个数=正方体的棱长总数乘棱长减2的差=12×(n-2);

3.一面涂色的小正方体的个数=正方体的面数乘棱长减2的差的平方=6×(n-2)2。

温馨提示：通过以上关于长方体和正方体内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。