角格点问题一般解法(角格点问题全解)

一道“角格点”经典难题的求解“说三法”

平面几何的有关“角格点”问题中，有许多简精经典的好问难题，同时会有许多独具匠心的求解方法。今有一道其的经典难题，来说说其的三种思考方法：

【例题】（如图）在△ABC中，点D为其内一点，且∠ABD=30º，∠DBC=40º，∠ACD=50º，∠DCB=20º，求：∠BAD的度数

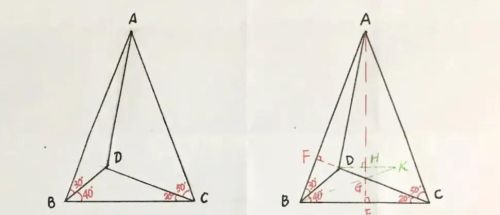
【思路一】（中垂线、等腰、全等）

（1）由已知可得：AB=AC，∠BAC=40º

（2）延长CD交AB于点F，则∠CFB=90º，又∠DBF=30º，∴FD=BD/2

（3）过点A作AE⊥BC，垂足为E，交CD于点G，则AE为BC边的中垂线，连BG，∴GB=GC，∴∠GBC=∠GCB=20º=∠GBD

（4）过点D作BC的平行线交AE于点H，并交BG的延长线于点K，即：DK∥BC，∴GH⊥DK

（5）易得：∠K=∠KBC=20º=∠DBK=∠KDG，∴BD=DK，GD=GK，所以GH垂直平分DK，∴DH=DK/2=BD/2=DF

（6）易证：Rt△AFD≌Rt△AHD（HL）

（7）所以：∠BAD=∠HAD=∠BAE/2=10º

【思路二】（中垂线，角平分线、正弦定理）

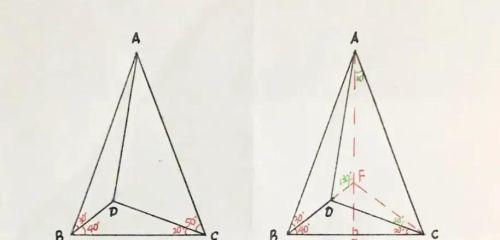
（1）易得：AB=AC，∠BAC=40º，作BC边上高AE，即AE为BC边上中垂线且平分∠BAC，∴∠BAE=∠CAE=20º

（2）延长BD交AE于点F，连FC，∴FB=FC，则∠FCD=20º=∠BCD，∠AFB=130º

（3）由角平分线定理得：BC/FC=BD/FD，即BD/FD=2EC/FC=2cos40º=2sin50º

（4）在△ABF中，根据正弦定理可得：AB/AF=sin130º/sin30º=2sin50º=BD/FD

（5）在△ABF中根据角平分线定理逆定理可得：AD平分∠BAF，∴∠BAD=10º

【思路三】（30º角、作正三角形、造外心）

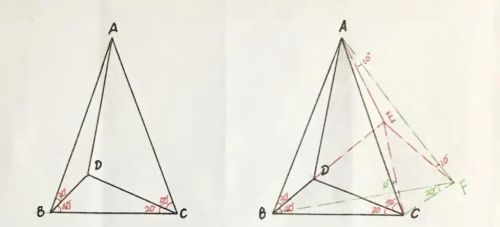
（1）由己知得：AB=AC，∠BAC=40º

（2）以AB为边（如图）作正三角形△ABF，连CF，∴∠FBC=10º，∠DBF=30º=∠DBA，∴BD为边AF的中垂线

（3）易得：AB=AF=AC=BF，∴点A为△BCF的外心，∴∠BFC=∠BAC/2=20º，∠CAF=20º

（4）作∠CAF的平分线与BD的延长线交于一点E，连EC、EF，则：∠CAE=∠FAE=10º，易证：△ACE≌△AFE（SAS），∴EC=EF，又中垂线BE，∴EA=EF=EC，∴∠ECA=∠EAC=10º

（5）易得：∠ECD=50º＋10º=60º=∠EDC，∴△EDC为正三角形，∴ED=EC=EA，则：点E为△ADC的外心，∴∠CAD=∠CED/2=30º

（6）故：∠BAD=40º－30º=10º

以上三法之分析，“道听度说”供参考。

温馨提示：通过以上关于一道“角格点”经典难题的求解“说三法”内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。