如何证明多项式函数(证明多项式定理)

这个证明会不会太无聊？证明多项式函数图像两端严格单调

多项式函数，比如一次函数，二次函数，三次函数等，这类函数的图像两端都是严格单调的。这么说，大家不会有意见吧。因为上面列举的函数图像，都是比较常见的，这个结论似乎是可以想象得到的。因此，如果让你证明多项式函数图像两端严格单调，你会不会觉得很无聊呢？

事实上，就算你能够想象得到，四次函数、四十次函数，乃至四亿次函数都符合这个规律，但想象的始终都只是想象的，想象是不能做为数学定理的依据的，这也是为什么“1+1=2”只能做为一个猜想，而不能称为哥德巴赫定理的原因。所以，证明多项式函数图像两端严格单调其实还是有必要的。

证明：对任一多项式p(x)来说，一定存在点x1与x2，使p(x)在(x1,+∞)与(-∞,x2)上分别严格单调.

注意，既然称为多项式函数，就排除了常量函数，因为常量函数既是增函数，也是减函数，但不严格单调。下面就是这个问题的证明过程：

证：记pn(x)=a0+a1x+a2x^2+…+anx^n, n≥1, an≠0, 【注意：除了an不等于0，a0,a1,…,an这些系数都是可以任取的】

当n≤2时, 成立！【这个证明过程比较简单，老黄就省略了】

可设pk(x)=a1+2a2x+…+jajx^k成立, (j=k+1). 【这是数学归纳法的开始】

则存在x=x0，使pk(x)在(x0,+∞)上严格单调, 不妨设为单调增.

记pj(x)=a0+a1x+a2x2+…+ajxj, 则pj’(x)=pk(x).【因为pk(x)中的系数都是任取的，所以pj(x)的系数也是任取的】

当pk(x0)>0时, pk(x)>0, pj(x)在(x0,+∞)上严格单调增;

当pk(x0)<0时, 因为lim(x→+∞)pk(x)=+∞, 所以存在x1∈(x0,+∞), 使pk(x1)=0,

在(x1,+∞)上, pk(x)>0，pj(x)严格单调增.

综上，当pk(x)在(x0,+∞)上严格单调增时, 存在x1∈(x0,+∞), 使pj(x)在(x1,+∞)上严格单调增.

类似可证当pk(x)在(x0,+∞)上严格单调减时, 也存在x1∈(x0,+∞), 使pj(x)在(x1,+∞)上严格单调减.

由数学归纳法的思想可知，对任一多项式p(x)来说，一定存在点x1，使p(x)在(x1,+∞)上严格单调.

同理可证，对任一多项式p(x)来说，一定存在点x2，使p(x)在(-∞,x2)上严格单调. 得证！

如果你爱动脑筋的话，应该可以发现，当最高次项的系数符号性质保持不变时，多项式pn(x)在(x1,+∞)上保持相同的单调性，(-∞,x2)上的单调性则是交错的。

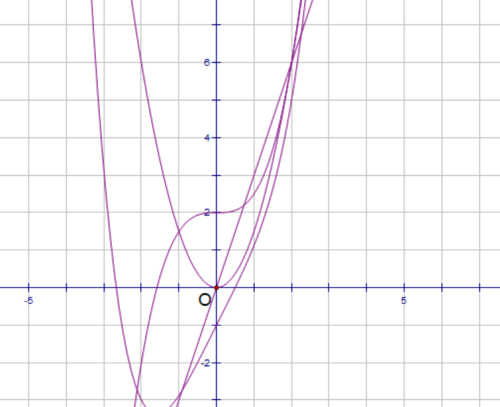
你可以尝试归纳出其中的更多规律。

温馨提示：通过以上关于这个证明会不会太无聊？证明多项式函数图像两端严格单调内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。