运用无穷多项方程的分析学(多项式无穷大比无穷大)

利用无穷大的定义，证明多项式函数两端严格单调

老黄已经在此前的作品中证明过“多项式函数两端严格单调”了，主要利用的是“导数的符号性质判断函数的单调性”以及函数的“零点存在性定理”的知识。但是老黄觉得还不过瘾，这次要利用“无穷大的定义”，来证明这个定理。

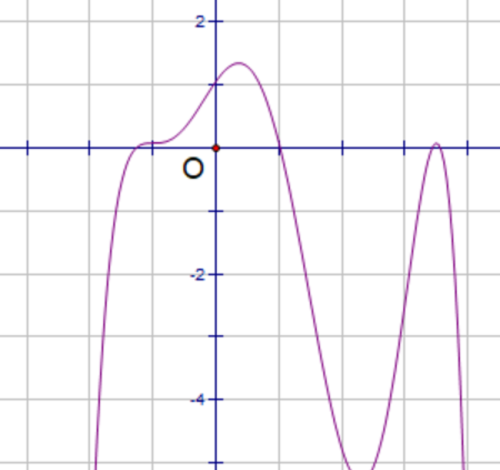
尽管“多项式函数图像两端严格单调”这个定理看起来好像由图像就可以想象出来，但想象不能做为定理的依据，而且证明过程和证明方法，以及用到的知识点才是重点。

证明：对任一多项式p(x)来说，一定存在点x1与x2，使p(x)在(x1,+∞)与(-∞,x2)上分别严格单调.

分析：我们可以记多项式p(x)的一般形式，其中最高次项系数a0≠0, 不妨设a0>0，a0<0也同理的。

当n=1时, p(x)=a0x+an是一条直线，在R上严格单调增，因此一定成立的！当n>=0时，

当n大于1时，求导，可以发现，导函数也是一个多项式函数，且次数比原函数少1.

如果n是奇函数，那么导函数p&39;(x)趋于正无穷大，即p&39;(x)>G>0. 取x1=M，x2=-M，那么多项式函数在两端就都是严格递增。

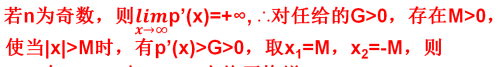
如果n是偶数，那么导函数p&39;(x)无穷大量，根据无穷大的定义：对任给的正数G，都存在正数M，使得当x>M时，p&39;(x)<-G<0，取x1=M，x2=-M，那么多项式函数在右端严格增，在左端严格减，

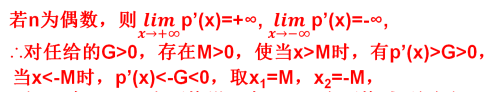
综上得证。

小伙伴们如果有兴趣，可以查阅老黄上一作品中的证法，比较一下两种证法，哪一种你更喜欢，它们运用的知识点是完全不同的哦。

温馨提示：通过以上关于利用无穷大的定义，证明多项式函数两端严格单调内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。