拉马努金无穷级数(拉马努金的函数)

拉马努金笔下的无限嵌套公式：“3=4”

起初数学家，对于这个奇怪的无限的1，2，3……,表达式难以理解，这是一个无限的嵌套公式，但拉马努金说它等于3，这里可以给你他的论点

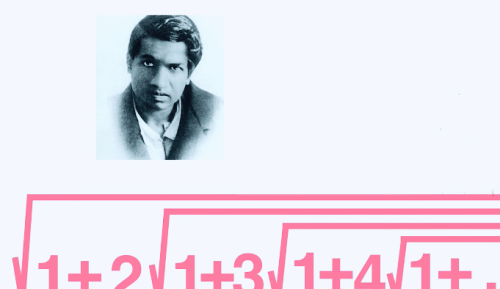
这个结论是个整数，在数学中也是是非常漂亮的

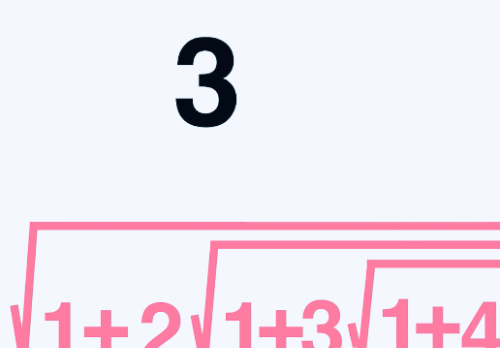
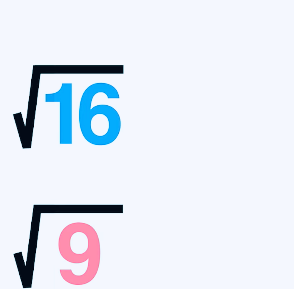
3等于根号9，9等于1加8

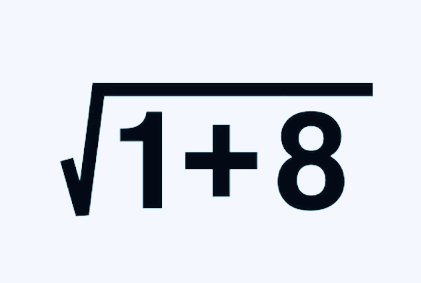
8等于2X4, 4等于16的平方根

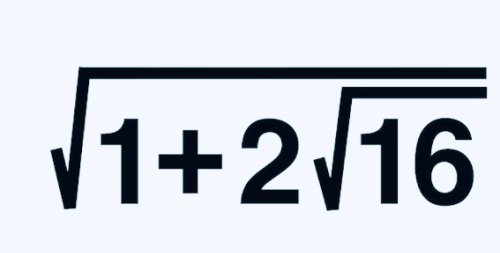
16等于1加15，15=3X5,

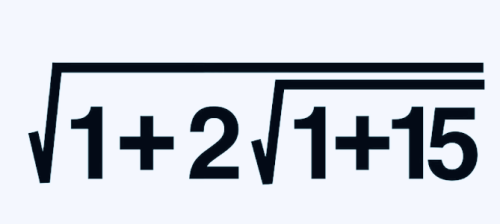
5等于25的平方根，我们这样继续下去，

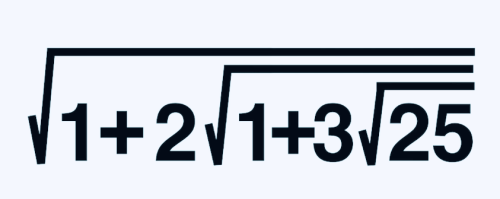
25等于1加24，24=4X6，6等于36的平方根

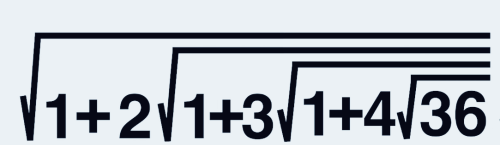
这样下去，很明显它们等于3

我们参照上式3的嵌套模式，可以写出4的嵌套公式，如下

我们同样写成1加2的模式，如下形式

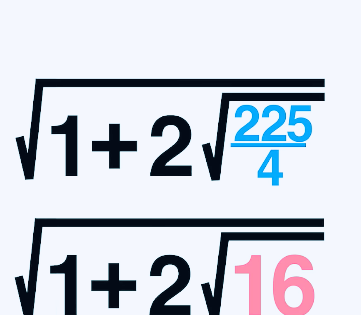
我们把数字写到前面，模仿3的嵌套模式

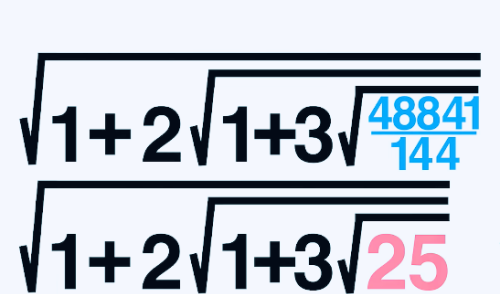
这样写下去，是不是会出现3=4的模式，当然不是

拉马努金对无穷级数很感兴趣，他是一个真正掌握这些原理的大师，如下只是他的一部分

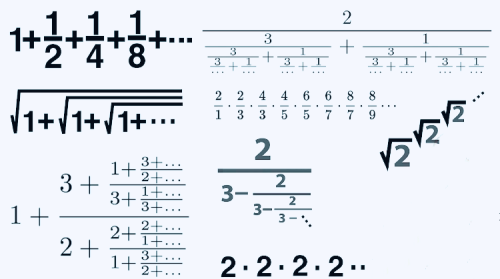
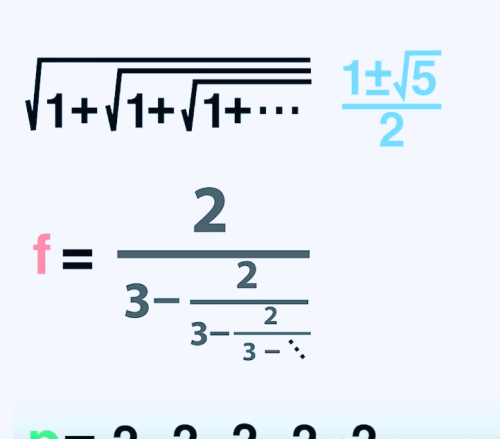
温馨提示：通过以上关于拉马努金笔下的无限嵌套公式：“3=4”内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。