交错代数 柔性定律(交错代数作者)

交错代数

话题：

小石头/编

引入

将 n元函数 f(x₁, x₂..., xn) 中的每个参数 xᵢ 由 实数集 ℝ 中的实数 变为 m维线性空间 V 中的向量，则 f 就变为 n重函数。

我们可以将 n重函数 f(x₁, x₂..., xn) 看做是 从 n个向量 x₁, x₂..., xn 组成的某种事物中提取某种特征值，例如：

就是提取的这 n个向量相加后向量的长度，如下图：

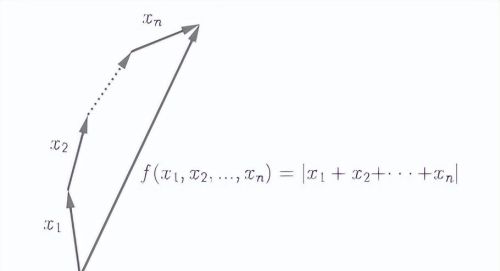
当然，这样的事物很多，其中的特征值就更多了，不过本篇关心的特征是：

以 n个向量为（共顶点）边 构成的 超平行体 的 超体积；

对于 2重函数 就是 平行四边形的面积，对于 3重函数 则是 平行六面体的体积，... ...，而，对 1重函数 则退化为 向量的长度，如下图：

下面，我们以 2重函数 为例子，看看这种 超体积函数 都有啥性质。

对其中 任意一个边 xᵢ 缩放 k（∈ℝ） 倍，即，k xᵢ，则 超体积 也跟着 缩放了 k 倍 ，如下图：

即有，

将任意一个边 xᵢ 分解为 两个边的向量和，即，令 ，相应的超平行体 也 分解为两个新的超平行，则 分解前后 超体积 保持不变，即，两个新的超平行体的超体积之合 等于 原超平行体的超体积，如下图：

即有，

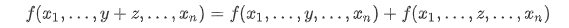任意两个不同边 xᵢ, xj （i≠j）如果重合，即，xᵢ = xj = ξ，则 超体积 为 0，如下图：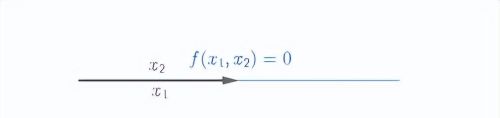

即有，

我们将 向量 x 的 缩放 kx 称为 数乘 运算，它 与 向量 的 加法 运算 x + y 一起 并称为 线性运算（V之所以叫做线性空间，就是因为其中向量具有 这两种 线性运算），进而 还称 具有 上面 性质 ⅠⅡ 的 多重函数 为 多重线性函数。如果 一个 多重线性函数，还满足 Ⅲ ，则被称为 交错的（alternating）。

需要注意：超体积函数 只是 众多 交错函数 中的 一个，实际上，超体积函数的线性运算结果 也是 交错的。

这些 交错函数，就是本篇讨论的主角。

初探

设 V 为 ℝ 上的 m维线性空间，对于 V上的 n重线性函数 f: V×⋯×V→ℝ，若任意两个参数值相同都会导致函数值为零，即，

任意下标 1 ≤ i ≠ j ≤ k，若 xᵢ = xj = ξ 有 f(⋯, xᵢ, ⋯, xj, ⋯) = f(⋯, ξ, ⋯, ξ, ⋯) = 0；

则称 f 是 交错的（alternating）。

对于交错函数 f，有，

f(⋯, xj, ⋯, xᵢ, ⋯) + f(⋯, xᵢ, ⋯, xj, ⋯) = f(⋯, xj + xᵢ, ⋯, xᵢ + xj, ⋯) = f(⋯, xᵢ + xj , ⋯, xᵢ + xj, ⋯) = 0

故，

即，

交换函数的任意两个参数，则函数值取反；

这称为 反对称的（或 反交换的 （anti-commutative））。

反过来，对于反对称函数 f，有，

½f(⋯, ξ, ⋯, ξ, ⋯) = -½f(⋯, ξ, ⋯, ξ, ⋯) ⇒ f(⋯, ξ, ⋯, ξ, ⋯) = ½f(⋯, ξ, ⋯, ξ, ⋯) + ½f(⋯, ξ, ⋯, ξ, ⋯) = 0

所以，交错的 就是 反对称的，反对称的 就是 交错的。

不妨设，交错函数最初传入参数时值为正，然后任意交换两个参数则值变为负，然后再交换则值又回到正，...，可见，交错函数的值 在 正与负 之间 交错出现，这就是 “交错” 二字得名的由来。

参数的交换就是参数位置的交换，我们 用 N={1, ..., n} 表示 n重交错函数 的 从左到右的 n 个参数位置， 用 (i, j) , i ≠j 表示 第 i 个参数 和 第 j 个 参数 相互交换，这称为 对换。

任意 多次 对换 的 结果，构成一个置换，表示为多个对换的复合，例如：σ = (2, 3)∘(1, 2) 就是先对换 1, 2 参数，再对换 2，3 参数的一个置换。当然 任意两个 置换 一样可以复合为一个新的置换。我们可以通过统计 一个置换 中 所含 对换的 个数，来得到 置换 所引起的 函数符号变化：

当 σ 是偶数个对换的复合 时，称 σ 为 偶置换，此时，函数符号不变，记为 +1；当 σ 是奇数个对换的复合 时，称 σ 为 奇置换，此时，函数符号改变，记为 -1；

若 将 n个位置上的全体 置换，记为 S(n) （这称为 对称群，不过大家不用理会它为啥是群，本篇文章用不到），则 上面 过程 可以构成一个 符号函数：

sign: S(n) → {+1, -1}, σ ↦ +1, σ 是偶置换 | -1, σ 是奇置换

很容易发现，sign 与 复合运算可交换，即有，

sign(τ∘σ) = sign(τ)∘sign(σ)

所以我们实际上只需要规定：

σ((i, j)) = -1

即可。

值得注意的是，一个置换的对换复合可以不同，进而对换个数也不一定相同，例如，上面的置换还可以写成 σ = (5, 4)∘(4, 5)∘(2, 3)∘(1, 2) ，但是可以证明，置换的奇偶性 保证不变，故上面 sign 的定义是 良好的。

若 让 置换是从 参数下标从小到大的，即，f(x₁, x₂..., xn)，的初始排列开始的变换，则 每个 σ 对应一个 n个参数的 全排列，此时我们用 σ(i) 表示这个全排列中 第i个位置的 参数 下标，则排列后的 函数记为 f(xσ(1)，xσ(2), ..., xσ(n)) ，进而最终得到：

​f(xσ(1)，xσ(2), ..., xσ(n)) = sign(σ)f(x₁, x₂..., xn) ①​

这表示了 交错函数 在参数任意 置换后 的函数值。

深入

我们知道，V上的 全体 n重线性函数（记为 ℒ(V,⋯,V; ℝ)） 是一个 线性空间，为此，将 n重线性函数看做向量（称为 张量），并且定义线性运算为：

加法：(f+g)(x₁, x₂, ..., xn) = f(x₁, x₂, ..., xn) + g(x₁, x₂, ..., xn)数乘：(kf)(x₁, x₂, ..., xn) = kf(x₁, x₂, ..., xn)

而对于其中任意交错函数，有，

(f+g)(⋯, ξ, ⋯, ξ, ⋯) = f(⋯, ξ, ⋯, ξ, ⋯) + g(⋯, ξ, ⋯, ξ, ⋯) = 0 + 0 = 0

(kf)(⋯, ξ, ⋯, ξ, ⋯) = kf(⋯, ξ, ⋯, ξ, ⋯) = k0 = 0

这说明，交错函数 对于线性运算封闭，故全体 交错函数 组成 ℒ(V,⋯,V; ℝ) 的一个线性子空间，记为 Altⁿ(V)。

诚然，并不是所有线性函数都是交错的，但是我们可以将任意线性函数 f 变为一个交错函数，方法如下：

将 f 的所有参数排列 交错相加，即，An(f)(x₁, x₂, ..., xn) = (1/n!) ∑σ ∈ S(n) sign(σ)f(xσ(1), xσ(2), ..., xσ(n))；

这很好理解，因为 对于 An(f) 中 任意 和项 的 任意 两个位置 ±f(..., xσ(i), ..., xσ(j), ...) 一定对应 位置互换的 和项 ∓f(..., xσ(j), ..., xσ(i), ...) ，于是当 两个参数 xσ(i)， xσ(j) 互换有，

± f(..., xσ(j), ..., xσ(i), ...) ∓ f(..., xσ(i), ..., xσ(j), ...) = -(∓ f(..., xσ(j), ..., xσ(i), ...) ± f(..., xσ(i), ..., xσ(j), ...) ) = - (± f(..., xσ(i), ..., xσ(j), ...) ∓ f(..., xσ(j), ..., xσ(i), ...) )

即，符号相反，是反对称的，每一个局部都是这样，所以整体 An(f) 就是 反对称的，我们称 An 为反对称化算子。

对于 p重线性函数 f 和 q重线性函数 g，如果 p = q = n ，我们可以 仿照 加法运算，定义 乘法，

(f×g)(x₁, x₂, ..., xn) = f(x₁, x₂, ..., xn)g(x₁, x₂, ..., xn)

但是当 p ≠ q 时，这种乘法就不灵光了，于是我们 改变思路，让 两个函数的 参数 从并联（要求参数个数一样），变成 串联（不要求参数个数一个），从而得到另一种乘法：

(f⨂g)(x₁, x₂, ..., xp, xp+1, ..., xp+q ) = f(x₁, x₂, ..., xp)g(xp+1, ..., xp+q)

因为 f和g 也被称为 张量，所有这种乘法称为 张量积。很显然，张量是一个二元映射,

⨂: ℒ(V,⋯p⋯,V; ℝ) × ℒ(V,⋯q⋯,V; ℝ) → ℒ(V,⋯p+q⋯,V; ℝ)

它将 一对 p和q重线性函数 (f, g)，映射为 一个p+q重线性函数 f⨂g。

注：为了强调 ℒ(V,⋯,V; ℝ) 中有 p 个 V，我们将其写成 ℒ(V,⋯p⋯,V; ℝ)；

因为 Altᵖ(V) 和 Altᶣ(V) 分别是 ℒ(V,⋯p⋯,V; ℝ) 的 ℒ(V,⋯q⋯,V; ℝ) 子空间，于是考虑 ⨂ 在 Altᵖ(V) × Altᶣ(V) 上的限制，

⨂|Altᵖ(V) × Altᶣ(V) : Altᵖ(V) × Altᶣ(V) → ℒ(V,⋯p+q⋯,V; ℝ)

注：找不到 q 的上标符号，用 ᶣ 代替。

我们希望 这个限制 的 值域 是 Altᵖ⁺ᶣ(V)，但是很可惜，两个交错函数的 张量积 并不一定是 交错的，不过我们可以利用上面定义的 反对称化算子，对 这个限制的结果 反对称化，从而使其变成一个 交错函数，这样我们就又定义一种新的乘法：

∧: Altᵖ(V) × Altᶣ(V) → Altᵖ⁺ᶣ(V)，(f, g) ↦ ((p+q)!/p!q!) Ap+q(f ⨂ g) = (1/p!q!) ∑σ ∈ S(p+q) sign(σ)f(xσ(1), ..., xσ(p))g(xσ(p+1), ..., xσ(p+q))

这称为 楔乘（也叫做 外积）。

楔乘的定义还可以优化，因为 f 和 g 已经 是 交错的了，它们是不需要反对称化的，这就是优化空间。实际上，S(p+q) 中每个全排列，可认为是由以下两步得来，

第一步：先将 1 到 p+q 个自然数 分为 分别含有 p 和 q 个数 的 左右两组；第二步：在两组内取各自的某个全排列；

对于任意分组，我们总能找到，使得：

σ(1) < ... < σ(p) 并且 σ(p+1) < ... < σ(p+q) 的全排列 σ ∈ S(p+q) ；②

此时，我们 令，

y₁ = xσ(1), ..., yp = xσ(p)，z₁ = xσ(p+1) , ..., zq = xσ(p+q)

则 楔乘定义式右边，保持分组不变的和式部分可写为，

(1/p!q!) ∑σ₁∈ S(p) , σ₂∈ S(q) sign(σ)(sign(σ₁)f(yσ₁(1), ..., yσ₁(p)))(sign(σ₂)g(zσ₂(1), ..., zσ₂(q)))

于是有，

= (1/p!q!) sign(σ)(∑σ₁∈ S(p) sign(σ₁)f(yσ₁(1), ..., yσ₁(p)))(∑σ₂∈ S(q) sign(σ₂)g(zσ₂(1), ..., zσ₂(q)))

又 因为 f 和 g 是交错性，根据 ① 上式，进而有，

= (1/p!q!) sign(σ)(∑σ₁∈ S(p) sign(σ₁)sign(σ₁)f(y₁, ..., yp))(∑σ₂∈ S(q) sign(σ₂)sign(σ₂)g(z₁, ..., zq))

= (1/p!q!) sign(σ)(∑σ₁∈ S(p) sign²(σ₁)f(y₁, ..., yp))(∑σ₂∈ S(q) sign²(σ₂)g(z₁, ..., zq))

= (1/p!q!) sign(σ)(∑σ₁∈ S(p) f(y₁, ..., yp))(∑σ₂∈ S(q) g(z₁, ..., zq))

= (1/p!q!) sign(σ)(p! f(y₁, ..., yp))(q! g(z₁, ..., zq))

= sign(σ) f(y₁, ..., yp)g(z₁, ..., zq)

= sign(σ) f(xσ(1), ..., xσ(p))g(xσ(p+1), ..., xσ(p+q))

而 楔乘定义右边和式，就是全部 保持分组不变的和式部分 之和，于是，若用 S(p, q) 表示全部满足 ② 的全排列，则楔乘定义可简化为：

f∧g = ∑σ ∈ S(p, q) sign(σ)f(xσ(1), ..., xσ(p))g(xσ(p+1), ..., xσ(p+q)) ③

我们称 S(p, q) 中的排列为 洗牌，形象的看，它是 含有 p 和 q 张扑克的 两叠牌，按照下图方式 进行的 洗牌，

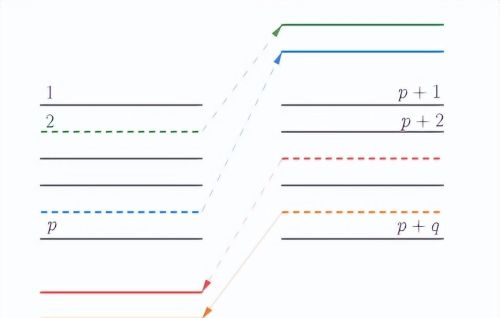
这与我们日常熟悉的洗牌方式不同。

（由于篇幅过长，先分个P，今天写不动了，之后有精力再继续写。）

温馨提示：通过以上关于交错代数内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。