阿氏圆相似证明(阿氏圆和相似)

中考几何压轴 81 几何与函数 相似比 求坐标方法 另 阿氏圆最值模型

中考几何压轴 81 几何与函数 相似比 求坐标方法 另 阿氏圆最值模型

这一系列，不限专题，解析系列经典几何题，提高几何分析解决问题能力。

题88. 《相似比到点坐标 · 阿氏圆最值》

如图，抛物线y＝ax²＋(a＋3)x＋3(a≠0)与x轴交于点A(4,0)，与y轴交于点B，在x轴上有一动点E(m, 0)(0＜m＜4)，过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过P作PM⊥AB于点M。

[1].求a的值和直线AB的函数表达式；

[2].设△PMN周长为C₁，△AEN周长为C ₂，若C₁/C ₂＝6/5，求m的值；

[3].在[2]条件下，将线段OE绕点O逆时针旋转得到OG，旋转角度为α（0＜α＜90°），连接GA，GB，求GA＋(2/3)GB的最小值。

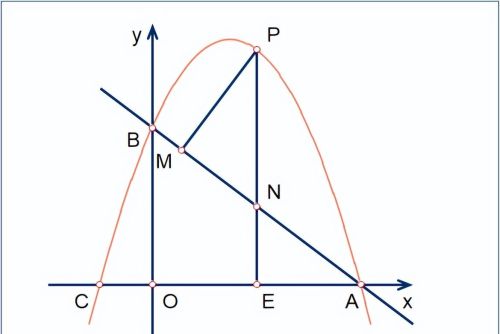
〖一般性提点〗

[1]. 由题设条件求点坐标，是二次函数/几何综合题不二的题型。其典型的方法有：

<1>. 求直线与二次函数交点，或求直线与直线交点；

<2>. 构建一线三直角结构，通过相似求点坐标；

然而，本题题设中根据三角形的相似比求点坐标，如果通过<2>不仅麻烦而且有点画蛇添足：既然已经有了相似关系，再构建一线三直角就多余了。

当已知相似比的时候，要通过坐标便捷表达线段长度，就要找到三角形内部线段之间的比值，从而通过与坐标轴平行的线段之比求得题设点坐标。详细内容参考题目解析。

〖题目解析〗

[1].

a＝-3/4；

L(AB)：y＝－3/4x＋3；

抛物线：y＝-3/4x²＋(9/4)x＋3；

[2].设△PMN周长为C₁，△AEN周长为C ₂，若C₁/C ₂＝6/5，求m的值；

易知△PMN∽△AEN，其相似比

λ＝C₁/C ₂＝6/5；

欲根据相似比求坐标，依本题特点，若能求得PN/NE的值是最便捷的。

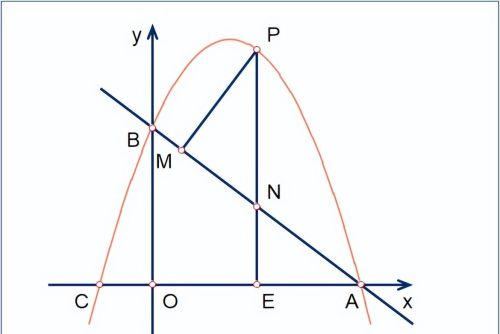
△PMN是Rt三角形，易知三边之比

MN∶PM∶PN＝3∶4∶5；

∴MN＝(3/5)PN； ①

又 ∵ △PMN∽△AEN

∴ MN/NE＝λ＝6/5； ②

由①、②最终得到：

PN＝2NE ③

线段长度表达：

E(m,0)、N(m,-3/4m＋3)、P(m, -3/4m²＋(9/4)m＋3)

PN＝-3/4m²＋(9/4)m＋3－(-3/4m＋3)＝-3/4m²＋3m；

NE＝-3/4 m＋3；

代入③，得

-3/4m²＋3m＝2(-3/4 m＋3)

解得 m＝2；(另一个舍去)

即 E(2,0)。

[3].在[2]条件下，将线段OE绕点O逆时针旋转得到OG，旋转角度为α（0＜α＜90°），连接GA，GB，求GA＋(2/3)GB的最小值。

显然，G是以O为圆心，以OE＝2为半径的圆在第一象限内的弧上的动点。如图。

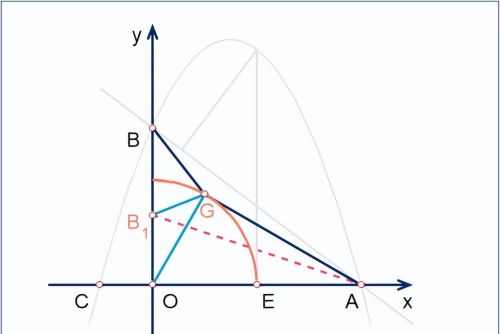
审核：

【1】定点A、B均在圆外；

【2】OG/OB＝2/3＝k＜1；可用阿氏圆方法求最值。

题解：

<1>. 在OB上取一点B₁，使得OB₁/OG＝2/3；

<2>. 连接OG、GB₁，构建子母三角形△OGB₁和△OBG；

<3>. △OGB₁∽△OBG:

☆ 共用角：∠GOB₁＝∠BOG；

☆ 由题设和作图：

OB₁/OG＝OG/OB＝2/3；

☆ 结果：GB₁＝(2/3)GB；

<4>. 连接AB₁，在△AGB₁中：由三角不等式：

GA＋GB₁≥AB₁

结果：

min(GA＋(2/3)GB)

＝min(GA＋GB₁)

＝AB₁

<5>. 求AB₁：

解Rt△AOB₁，得

AB₁＝4√10/3；

所以 min(GA＋(2/3)GB)＝4√10/3

温馨提示：通过以上关于中考几何压轴 81 几何与函数 相似比 求坐标方法 另 阿氏圆最值模型内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。