求相似比的方法(相似比例题)

一道初中几何题-求相似比的和

在三角形ABC中，点E在变AB上，并且有AE：EB=1:3，点D在变BC上，并且CD：DB=1:2， F是AD和CE的交点，那么计算下列线段比值的和：

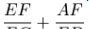
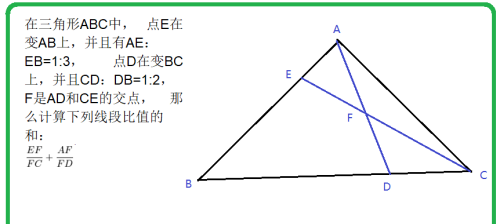
解：这是一个利用相似形求线段的相似比的问题，是一道简单的初中几何题。

如图，建立辅助线EQ平行于BC， DK平行于AB，

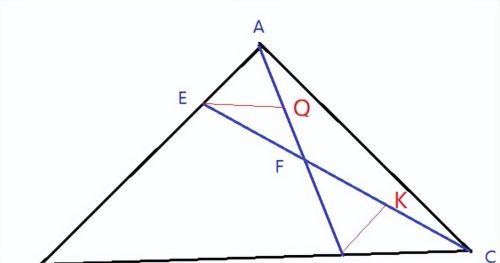
这样就会形成几组相似三角形。

因为三角形AEF相似于三角形DKF，所以有：

AF/FD=AE/DK

根据已知AE：EB=1:3，即AE=BE/3,

将AE=BE/3带入上面的比例式有：

AF/FD=BE/3DK (1)

但三角形BEC相似于三角形DKC，所以有：

BE/DK=BC/DC,

根据已知CD：DB=1:2，也就是BC=3DC，带入后，

BE/DK=3DC/DC=3,

将此式带入（1）中可得：

AF/FD=1:1=1

利用同样的方法计算EF/FC.

因为三角形EQF相似于三角形CDF，所以：

EF/FC=EQ/CD,

将CD=BD/2 带入上面的式子：

EF/FC=2EQ/BD （2）

而三角形AEQ相似于三角形ABD，所以有：

EQ/BD=AE/AB=1/4

将此式带到（2）中，即得出：

EF/FC=1/2

最后：

EF/FC+AF/FD=1+1/2=3/2

温馨提示：通过以上关于一道初中几何题-求相似比的和内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。