复数的性质总结(共轭复数的性质)

复数的性质

在数轴上负整数填补了正整数留下的空白，有理数填补了整数的空白，无理数填补了无理数的空白，这样实轴上充满了无数的数，那么一定有数来填满实数的空白，这种数就是复数。关于复数的由来有几百年的历史，最早是在求一元二次方程ax2+bx+c=0的根，如果判别式Δ=b2-4ac＜0时2在实数范围内则无解，比如x2+1的解按公式求得

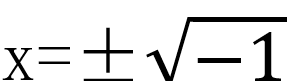
这在实数范围内是不可理解的，后来数学家们引进一个“想象”的数字i,它来自英语中的imaginary的首字母，把

，

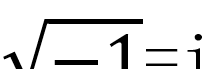
就解决了判别式小于零时，一元二次方程无实数解的问题。我们把i 称为单位虚数。那么=7i.

虚数 i 满足如下基本式子：

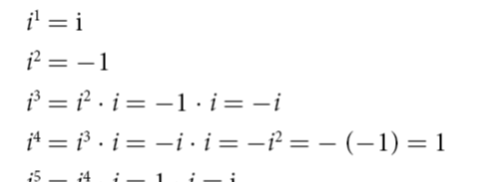
虚数 i 的定义

由此可见i的幂变换是每四个幂值为一个循环。

复数是一个实数与一个虚数的和，其标准写法为a+bi, 其中a是实部，b是虚部。整个复数集构成一个平面叫复平面，它在直角坐标平面是个点，x轴称为实轴，y轴为虚轴，如图复数-2+3i。

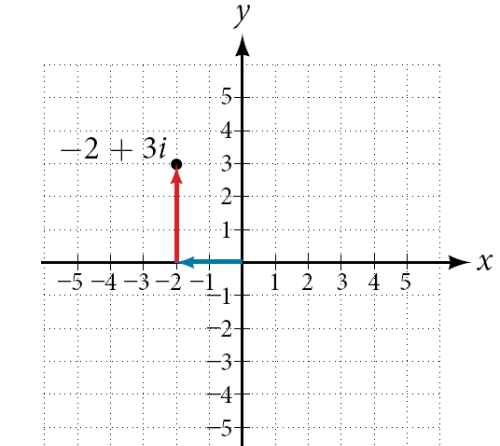
复数的一点

复数是可以进行加减乘除，乘方及开方的运算，本文不讨论复数的开方。

1. 复数的加减法运算，即两个复数的实数部分和虚数部分各自相加减

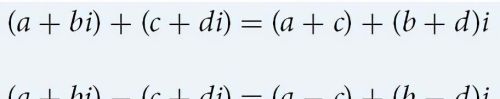
复数相加减

2. 复数的乘法运算，其与普通的代数运算完全相同：

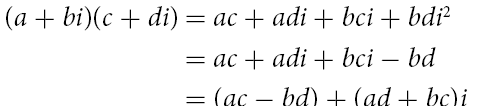
复数的乘法运算

3. 复数的除法运算，分母中的a和b 都不等于0，我们把a-bi叫做a+bi的共轭复数，为了消除分母中的虚数，要分子分母同时乘以分母的共轭复数，如下面的运算，

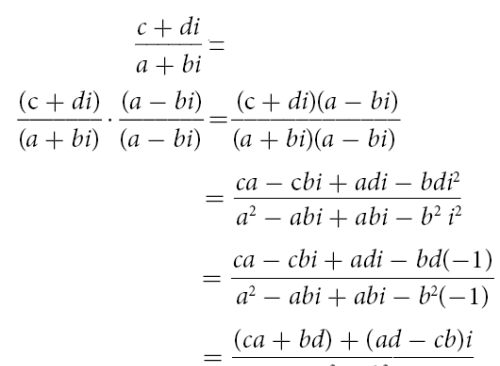
复数的除法运算

4. 复平面上的一个点可以看成是起点为原点的一个向量终点，这样就可以在复平面上进行向量的运算。

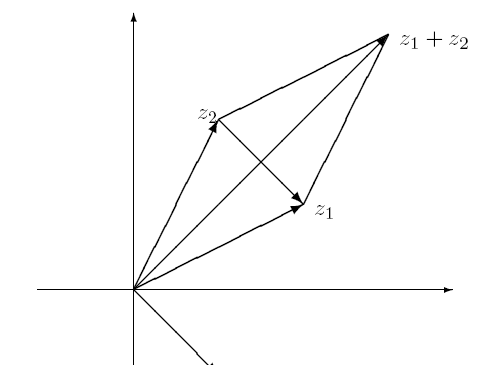
复平面上向量的加减

1. 复数的模

如果z = x + iy, 定义

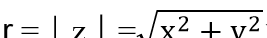
模的公式

为复数z的模。图中的θ角叫幅角，它的大小为记做argz =θ+2kπ, k属于整数，若-π＜θ≦π，则称为主幅角，记为Argz, 同时

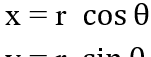
复数的极坐标表达

，那么复数又可以表示成：

z = r cosθ+ ir sinθ= r(cosθ+ i sinθ)，这是复数的极坐标形式或幅-幅角形式。

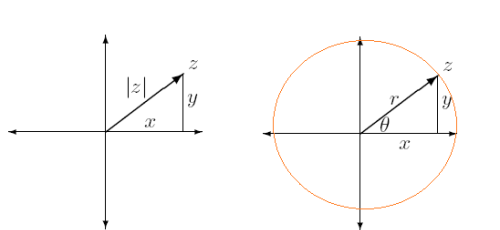
复数的模和幅角

z = x + iy的共轭形式记作

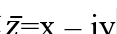
共轭复数

记z的倒数为,

很容易证明以下的模的等式：

复数的特性

6. 利用复数的模形式，可推出复数之积的模角等于两个复数的模角之和。

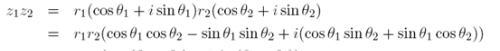
其余的可以自行推导：

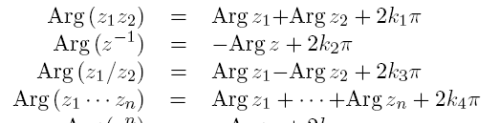
7. 棣美弗（De Moivre）定理：如果n是整数，又如下等式，它是上述式子的推广。

最后谈一下非常简单的复数 f(x) = x2 + c点集形成的复杂图形，这是一个迭代的运算，如果初始x0=0, 让：

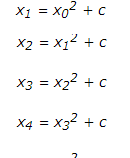
这种迭代一直进行下去，在复数c取某些定数的情况下，会形成曼德博点集，是一种在复平面上组成分形的点的集合，以数学家本华·曼德博的名字命名。利用计算机迭代并着色形成下列图形。

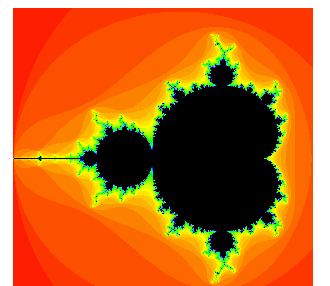
曼德博分形图

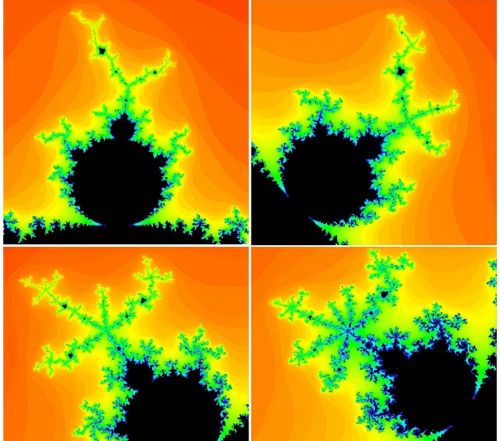
局部放大

温馨提示：通过以上关于复数的性质内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。