电动力学 电磁场(电动力学和电磁场理论)
神奇的电磁世界:电动力学(电荷和电场)
电荷和电场

各位小伙伴如果喜欢的话多多关注、点赞、转发哦,谢谢大家啦!
从这一期电动力学专题,我们将开始正式地对电磁世界进行探索,各位小伙伴请紧握扶手,我们出发咯!
(因为咸鱼作者本身是物理本科在读,所以对一些内容掌握的也有所欠缺,更新不稳定是因为在写的时候一些不熟练的地方还需要多看一下,物理很有趣但也需要严谨地对待,希望大家体谅一下,谢谢大家)
库仑定律
1785年,库仑通过实验发现,真空中静止点电荷Q对另一个静止点电荷Q&39;的带电量,r为Q指向Q&39;的距离,ε0为真空介电常数,ε0≈8.85×10^-12 C²/N。
针对一对点电荷时,库仑定律成立,那么若是有多个点电荷同时存在时,会有什么结果呢
实验结果告诉我们,当有多个点电荷同时存在时,每一个点电荷受到的作用力为其他点电荷对其单独的作用力的线性叠加,若该点电荷所带电量为Q,那么我们就能得到:
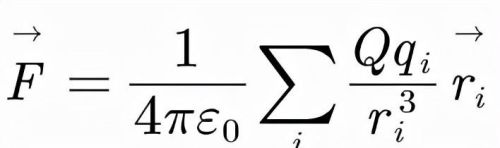
得到叠加原理之后,我们就可以很容易地处理一些连续带电体的问题:
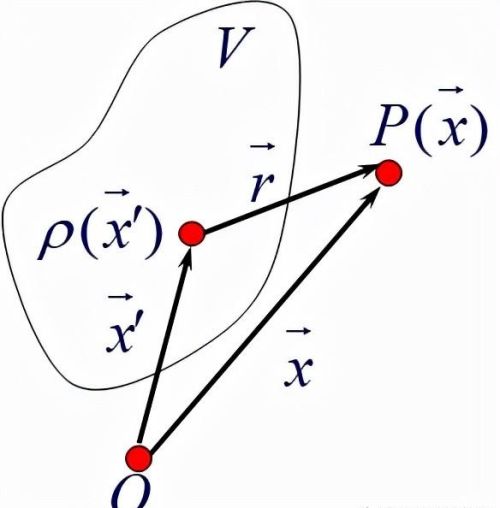
如图,存在电荷连续分布于空间某一区域V内,那么我们可以取体积元dV&39;内所含的电荷dQ等于该点的电荷密度ρ(⃗x&39;,即:
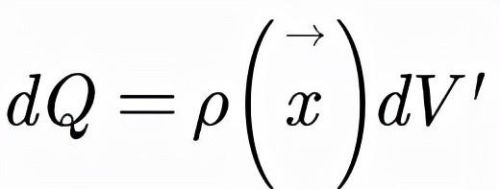
假设P点的电荷所带电荷量为q,那么我们根据库仑定律和叠加原理,就能得到静电力的大小为:
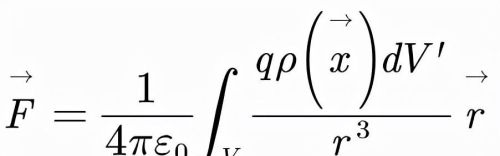
库仑定律是实验定律,没有解决电荷间作用力的物理本质问题。对之有不同的两种物理解释:(1)电荷之间是直接的超距作用;(2)电荷的相互作用是通过电场来传递的。我们不能单纯由静电现象判断哪一种解释是正确的。在运动电荷的情况下,两种观点就显示出不同的物理内容。而实践证明通过场来传递相互作用的观点是正确的。
那么这个“场”是什么?从库仑定律中我们可以看出,假如点电荷A带电量一定,那么对于点电荷B来说,它所受的静电力的大小与它自身的带电量成正比,于是我们就可以引入一个新的物理量:E=F/q
这里的E与存在于该点的电荷并没有什么关系,而是表示空间中的其他电荷在此处产生的效果。我们就把E称为电场。
我们根据定义很快就能得到点电荷产生的电场:
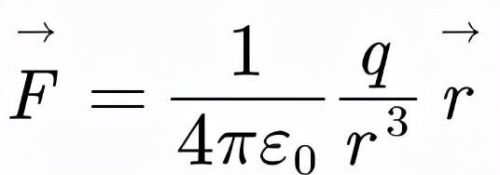
同理,对于连续带电体产生的电场我们也有:
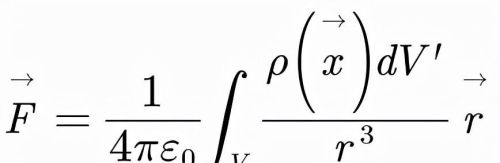
高斯定理和电场的散度
当我们得到电场之后,不可避免的,我们就想要去了解电场的图像是怎么样的,因此我们很自然的就想到了去看看电场的散度和旋度是怎么样的。
在高中物理中我们知道,电通量Φ=E·S,即电场强度乘以被电场线穿过的平面的面积。那么假如我们有一个闭合曲面S包围着点电荷Q,闭合曲面的面元为dS。很显然,电场线以点电荷为源,向四面八方发散,从闭合曲面的角角落落传出,我们根据电通量Φ=E·S便能很自然的得到点电荷产生的电场为面积分:
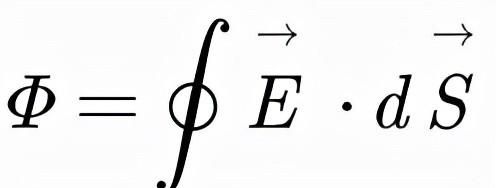
我们将E的表达式代入进行积分(dΩ为立体角元)就能得到:
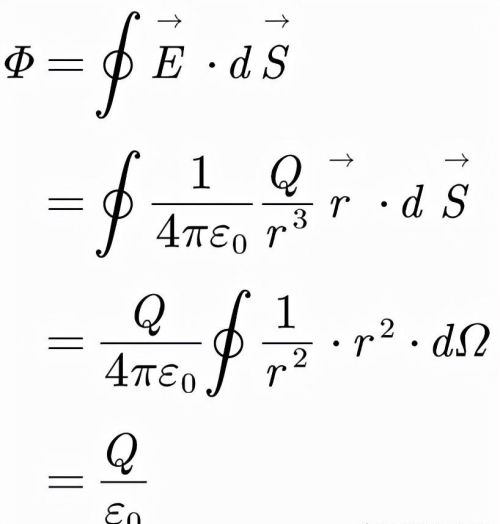
假如电荷不在闭合曲面内,那么电场线穿入闭合曲面后再穿出,对于闭合曲面的电通量没有贡献,因此Φ=0。
假如闭合曲面内有多个点电荷,显然它们的电场线都将穿过闭合曲面,所以就有:
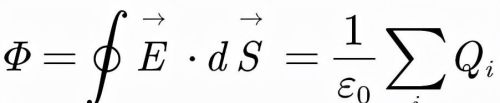
如果闭合曲面内电荷连续分布在空间中,我们则可以得到:
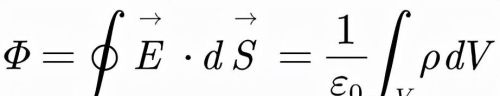
其中,ρ是电荷密度,V是闭合曲面包围的体积,显然ρ的体积分就是V内总电荷量。这也是静电场高斯定理的积分形式。
根据高斯公式我们知道,E的面积分等于E的散度的体积分,即E·dS=∇·EdV,假如我们让V不断缩小,最终我们就有:
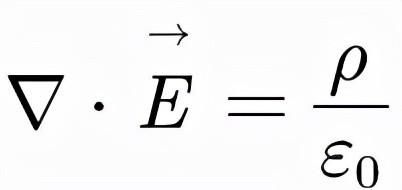
这就是静电场高斯定理微分形式,在这里它的物理意义是说明:静电场是一个有源场,电荷是电场的源点,电场线从正电荷出发到负电荷结束。
静电场的旋度
接下来我们来探究一下静电场的旋度∇×E,这个物理量表示的意思是静电场是否有涡旋状结构,简单来说就是静电场的电场线是不是会打转。
我们首先来看一下由点电荷激发出的静电场,其电场强度E对任一闭合回路的环量,结合库仑定律我们有:
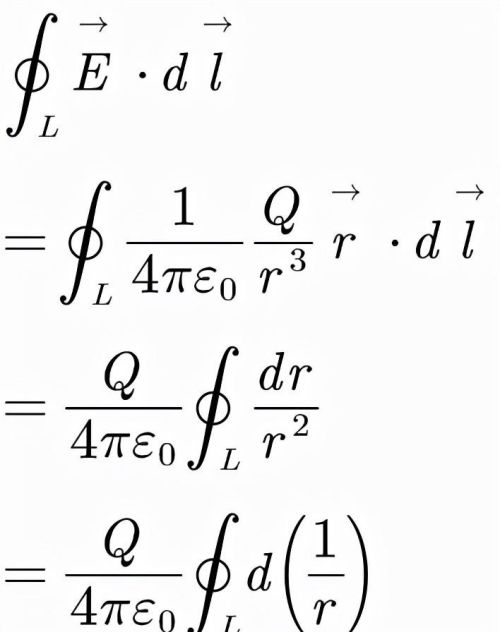
最后这个积分的被积函数是一个全微分,而由于绕了闭合回路L一圈以后,相当于又回到原点,函数1/r的值并未发生改变,所以我们就可以得到这个回路积分的结果为零,因此,我们有:
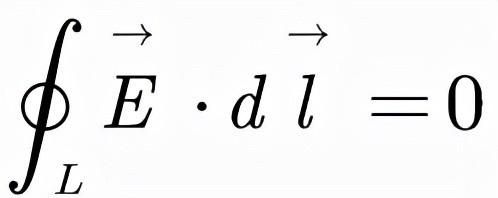
我们成功证明了点电荷的电场环量为零;而对于多个点电荷形成的电场,由于每个点电荷的电场环量均为零,根据叠加原理我们可以得到总电场的环量也为零。
在这里我们利用高数中学过的斯托克斯公式,根据斯托克斯公式我们可以给出:
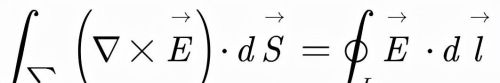
我们把回路L不断缩小,最终我们可以得到:
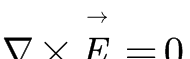
这个式子告诉我们静电场是一个无旋场,电场线并不会首尾相接地打转。
下期预告
在下一期的电动力学专题中,我们将会简单地了解电流和磁场,那么它们又具有怎么样的性质呢?各位对电磁世界好奇的小伙伴,我们下期专题见啦,喜欢的话记得点一下关注哦!
编 辑|笨笨
校 对|笨笨
审 核|笨笨

温馨提示:通过以上关于神奇的电磁世界:电动力学(电荷和电场)内容介绍后,相信大家有新的了解,更希望可以对你有所帮助。