傅里叶变换的虚数部分(虚数傅立叶变换)

傅里叶变换中的虚数j是什么意思

先理解一下虚数i的意义：

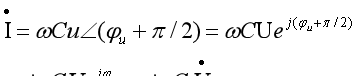
图1

其中的虚数 j 按照欧拉公式

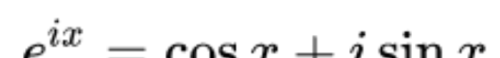
j=e^(jpi/2),那么图1就表示电流超前电压的相位90度。

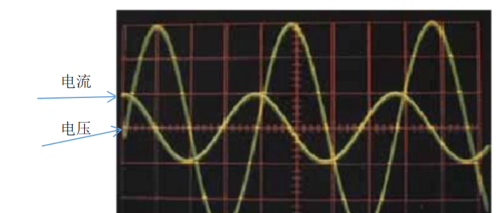
上图为实验验证。

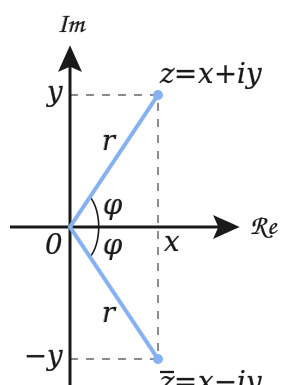
复平面

再看复平面，由于j=e^(jpi/2)，1=e^(j0),因此复平面上的实轴和虚轴本身就表示存在着pi/2的相位差。

再看傅里叶级数的三角形式：

从上图可以看到，相同频率的正弦和余弦谐波的不同系数

导致了相位的产生：

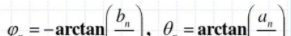
再看傅里叶级数的指数形式：

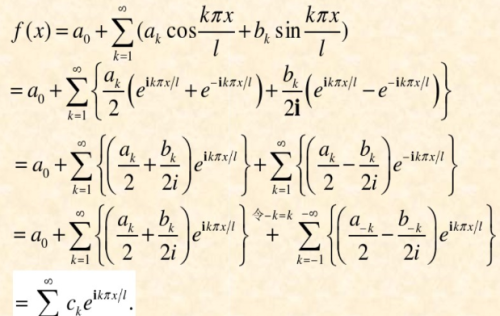
上图的系数ck是形如a+bi的复数，而a+bi是存在相位的，也就是说，在傅里叶级数的指数形式中，相位通过虚数 j 转移到了它的系数中去了。

至于其核函数

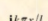
图2

按照欧拉公式，我们可以认为，函数f(x)展开以后，其余弦和正弦谐波分别被放到了复平面上相位差为pi/2的实轴和虚轴上面去了。

至于这样做的意义就在于，图2中的指数函数间的乘除运算要比三角函数方便得多。

温馨提示：通过以上关于傅里叶变换中的虚数j是什么意思内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。