初中数学抽屉原理(抽丝剥茧的推理)

抽丝剥茧，详细解析初中数学题68

如图所示,在△ABC中, ∠B=2∠C, AD⊥BC, 垂足为 D，M是BC 的中点,AB=10 cm,求 MD 的长。

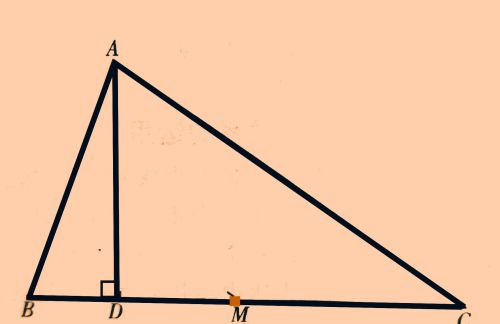
解析：1.凡是命题中的已知条件，

都不是摆设，

肯定有它的作用，

即使看起来孤零零的，

就像本题中M是BC的中点，

别小看它，

它是本题破题的关键。

我们只需找到AB的中点N，

将M与N连接起来，

那么MN就是△ABC的一条中位线。

这样一来，

即有了平行关系MN∥AC，

又有了比例关系，

还有了等角关系∠BMN=∠C

如下图所示。

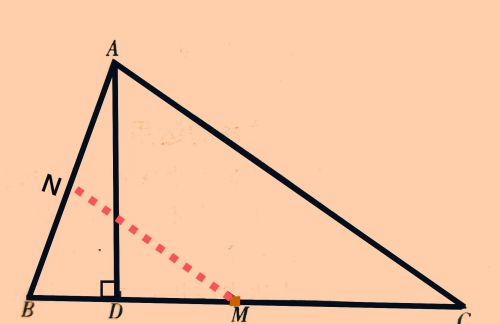
2由已知条件AD⊥BC可知，

△ADB是直角三角形，

因为N是斜边AB的中点，

那作用就大了去了。

如果把ND连接起来，

则有AN=BN=ND=AB/2=10/2=5㎝。

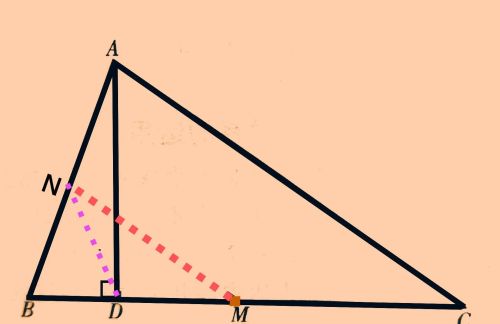
在等腰△NBD中，

∠B=∠BDN，

而∠BDN=∠DMN+∠DNM，

而∠DMN=∠BMN=∠C，

所以∠BDN=∠C+∠DNM，

所以∠B=∠C+∠DNM。

3由已知条件可知，∠B=2∠C，

所以2∠C=∠C+∠DNM，

所以∠C=∠DNM，

这真是一个奇妙的存在，

竟然导出了∠C=∠DNM，

而∠C=∠DMN，

所以∠DNM=∠DMN，

所以△MDN是等腰三角形，

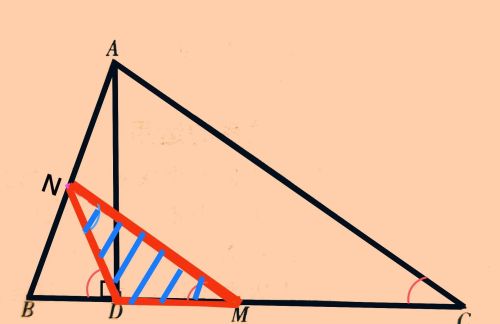
所以ND=MD，

而ND=AB/2，

AB=10㎝，

故MD=5cm。

温馨提示：通过以上关于抽丝剥茧，详细解析初中数学题68内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。