从1开始的连续奇数求和公式(从1开始的连续奇数的和)

从1始连续奇(单)数的和是多少 如何计算

从1始连续奇(单)数和是如何简算?(单数又叫奇(qi)数。)列式为:

1+3+5+7+9+……=?

很复杂吧？那么，我们从简单的开始。

1+3=4，没问题吧！我们把这个算式与图形结合起来研究这个问题。

用一个方块表示加数1，三个方格用下图表示。

把1个方格与3个方格合并起来就变成了一个边长为2的正方形。

这个正方形里包含2×2个正方形。那么，1+3=2×2=4.

同理：1+3+5，用下图来表示为：

合并后变成一个边长为3的正方形，一共有3×3=9（个）正方形。

那么，1+3+5=3×3=9.

观察：1+3=2×2=4，1+3+5=3×3=9 ，第一个算式有2个加数，结果是2×2，第二个算式有3个加数，结果就是3×3。可以猜想：1+3+5+7是不是4×4=16呢？加一下验证，的确是。用图表示也得出同样的结论。

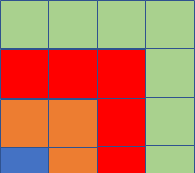
由此，我们可以推论：从1加起的连续奇数的和就是所有加数个数的平方。

那么，加数的个数在很少的情况下数一数可以搞定它，但遇到:

1+3+5+7+……+99

算式中有几个加数，怎么知道呢？

让我们来观察下面一组算式:

1+3(加数个数为2，末数是3，(3+1)÷2=2)

1+3+5(加数个数为3，末数是5，(5+1)÷2=3)

1+3+5+7(加数个数为4，末数是7，(7+1)÷2=4)

由此可得:加数个数(n)=(末数+1)÷2。

这样，

1+3+5+7+……+99=(99+1)÷2×[(99+1)÷2]=50×50=2500

总结:1+3+5+……+(2n-1)=n×n（n为加数的个数。）

拓展应用:利用上面的方法计算下面算式的和。

1+3+5+7+…+19+17+15+…+3+1

2+4+6+……+98+100

11+13+15+……+199

欢迎在评论区交流。

温馨提示：通过以上关于从1始连续奇(单)数的和是多少 如何计算内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。