皮尔森相关系数原理(皮尔森相关系数多少具有相关性)

十分钟了解皮尔森（pearson）相关系数

最早接触pearson相关系数时，是在大学《概率论与数理统计》课本中，后来从事数据分析挖掘相关的工作，经常会用到评价两组数据之间的相关性，于是找到了皮尔森（pearson）相关系数。其实，还有一种相关系数斯皮尔曼（spearman）相关系数，肯德尔（kendall）相关系数。

在这三大相关系数中，spearman和kendall属于等级相关系数亦称为"秩相关系数"，是反映等级相关程度的统计分析指标。今天先不介绍。

今天先聊一下比较常用的pearson相关系数。

用数学公式表示，皮尔森相关系数等于两个变量的协方差除于两个变量的标准差，先看一下公式：

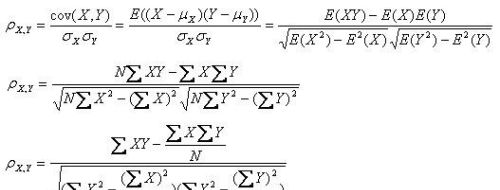
pearson是一个介于-1和1之间的值，用来描述两组线性的数据一同变化移动的趋势。

当两个变量的线性关系增强时，相关系数趋于1或-1；

当一个变量增大，另一个变量也增大时，表明它们之间是正相关的，相关系数大于0；

如果一个变量增大，另一个变量却减小，表明它们之间是负相关的，相关系数小于0；

如果相关系数等于0，表明它们之间不存在线性相关关系。

pearson相关系数在python中的实现：

1，numpy库中实现：

相关系数的对角矩阵

2，在scipy中实现，主要是在stats包中实现

得到的结果是一个元组，第一个元素是相关系数，第二个是P值，p-value越小，表示相关程度越显著。

3，在pandas中运用，日常处理数据都是用pandas，这个当然少不了喽

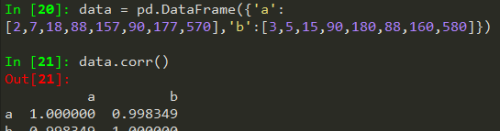
得到的也是一个相关系数数据

皮尔逊相关系数的适用范围：

当两个变量的标准差都不为零时，相关系数才有定义，皮尔逊相关系数适用于：

1. 两个变量之间是线性关系，都是连续数据。

2. 两个变量的总体是正态分布，或接近正态的单峰分布。

3. 两个变量的观测值是成对的，每对观测值之间相互独立。

温馨提示：通过以上关于十分钟了解皮尔森（pearson）相关系数内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。