利用轴对称的性质求线段最值(轴对称线段最短问题)

「初中数学」利用轴对称解决常规的线段和最值问题

用轴对称思想解决线段最值问题是常用的方法，本质是利用三角形三边关系或两点之间线段最短解决问题，即化折为直。常见的类型归纳为五种：即两定一动型，一定两动型，两定两动型，两定滑动型（架桥），三动型等。

类型一：两定一动型

【模型介绍】已知直线l同侧有A,B两点，在l上找一点P，使得PA+PB最小。

作法：作点A关于直线l的对称点A',连接A'B，与直线l的交点就是点P，线段A'B的长度即为最小值。

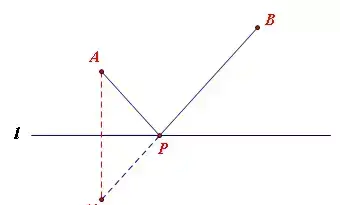
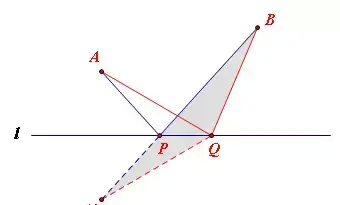
验证：如图，AQ+BQ=A'Q+BQ>A'B

【例1】(难度系数☆)如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值是__________.

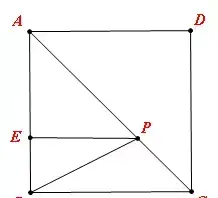
【分析】这是两定一动模型，需要作一个定点关于动点所在直线的对称点，根据本题图形特征，B点关于AC的对称点恰好是C点，连接CE，CE即为所求的最小值。

【答案】10

【例2】(难度系数☆)如图，在平面直角坐标系中，A（2，1），B（5，5），P是x轴上一动点，当PA+PB值最小时，求点P坐标

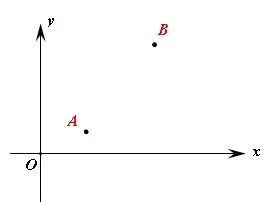
【分析】这是两定一动模型，作A点关于x轴的对称点A'，A'B与x轴的交点即为P，P点坐标可以用直线解析式或勾股定理求，初三学生也可用相似。

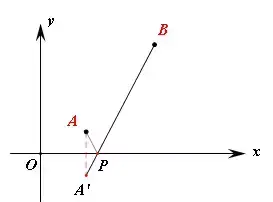
【答案】P（2.5，0）

类型二：一定两动型

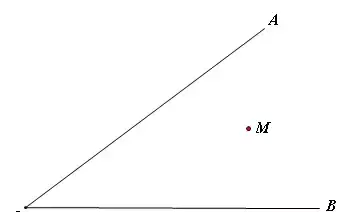
【模型介绍】已知，在∠AOB内有一点M，在边OA,OB上分别找点P,Q，使MP+MQ+PQ最小。

r

作法：作M关于OA的对称点M‘，关于OB的对称点M''，连接M'M''，交OA于点P，交OB于点Q，此时则MP+MP+PQ的值最小，最小值即为线段M'M''的长。

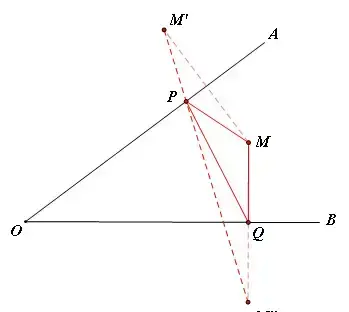
验证: 如图，OA上取一点P',OB上取一点Q'，连接M'P',M''Q',则MP'+MQ'+P'Q'=M'P'+M''Q'+P'Q'>M'M''(两点之间线段最短)

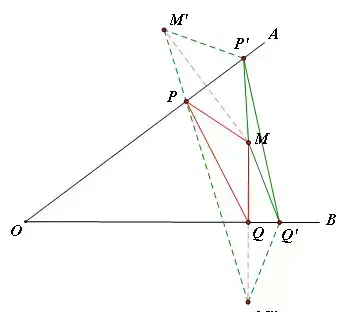
【例3】(难度系数☆☆)五边形ABCDE中，∠A=120°，∠B=∠E=90°，AB=BC=1，AE=DE=2，在BC、DE上分别找一点M、N，使得△AMN的周长最小，则△AMN周长的最小值为____.

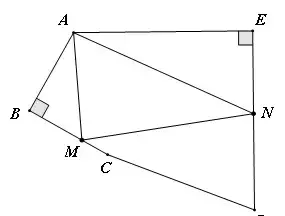
【分析】这是一定两动模型，作点A关于BC的对称点A’，关于ED的对称点A''，连接A'A''，交BC于M，交ED于N，此时△AMN的周长最小，最小值即为A'A''的长。解含120°的△AA'A'‘即可求出A'A''。

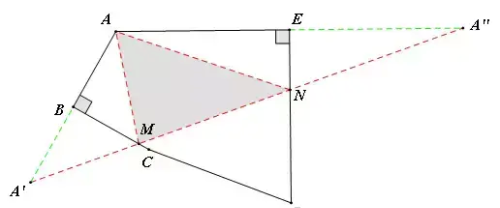
【答案】2√7。倘若追加一问：此时∠AMN+∠ANM=_____°，你能答对吗？

【例4】(难度系数☆☆)如图，点P是四边形ABCD内一点，BP=2，∠ABC=60°，分别在边AB,BC上作出点M,N，使△PMN的周长最小，求这个最小值。

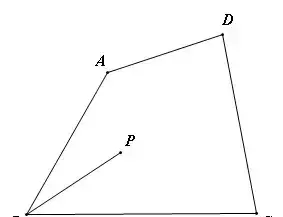
【分析】这是一定两动模型，作点P关于AB的对称点P’，关于BC的对称点P''，连接P'P''，交AB于M,交BC于N，此时△PMN的周长最小。在△BP'P''中，∠P'BP''=120°，BP'=BP=BP''=2，P'P''的长度很容易求。

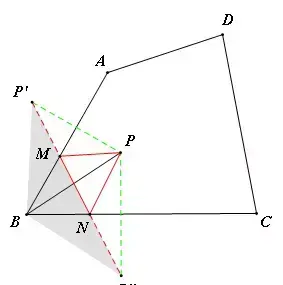
【答案】2√3

【例5】(难度系数☆☆☆)如图，在矩形ABCD中，AB=20，AC=10，若在AC,AB上各取一点M,N，求BM+MN的最小值。

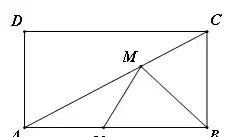
【分析】这是一定两动型的变异模型，其变化在于：①定点与动点所在的直线在同一直线上，②求的是两条线段和的最小值，而不是周长最小值。要使BM+MN的值最小，应设法把折线BM+MN拉直(即化折为直)，从而想到用轴对称性质来做。画出点B关于直线AC的对称点B1，则B1N的长就是最小值；又因为N也是动点，所以，当B1N⊥AB时这个值最小，利用勾股定理和三角形面积公式可以求得这个最小值，初三的同学也可以用相似或三角函数求解。

【解答】作B点关于AC的对称点B1,再过B1作AB的垂线，垂足为N，与AC的交点为M，此时BM+MN的值最小。

类型三：两定两动型

【模型介绍】在∠MON内有两点P,Q，在边OM,ON上分别找点R,S，使得PR+RS+SQ+PQ最小。

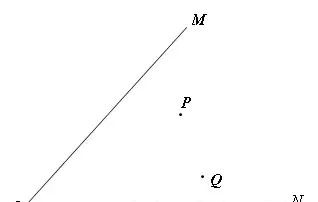
作法：作点P关于OM的对称点P',点Q关于ON的对称点Q'，连接P'Q'，与OM,ON的交点就是R,S，此时四边形PRSQ的周长最小。

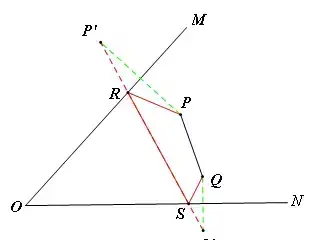
验证：在OM上取一点R‘，ON上取一点S’，则PR'+R'S'+QS'=P'R'+R'S'+S'Q'>P'Q'(两点之间，线段最短)

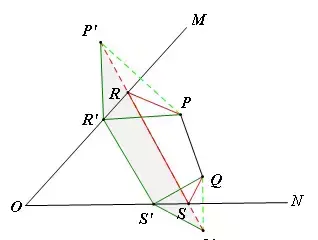
【例6】(难度系数☆☆)如图，∠MON=30°，A在OM上，OA=2，D在ON，OD=4，C在OM上的任意一点，B是ON上的任意一点，则折线ABCD的最短长度为______.

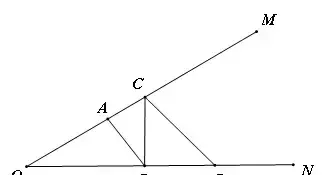
【分析】作D关于OM的对称点D'，A关于ON的对称点A‘，连接D'A'，交OM于C，交ON于B，则AB+BC+CD的值最小，最小值即为D'A'。此时∠D'OA'=90°，OD'=4,OA'=2，D'A'=2√5

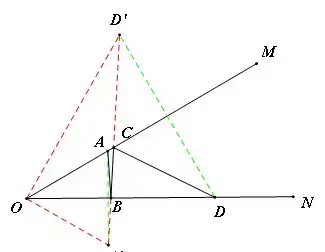
类型四：两定滑动型（架桥）

【模型介绍】在A和B两地之间有一条河，现要在这条河上建一座桥CD，桥建在何处才能使从A到B的路径最短？（假定河的两岸是平行的直线，桥要与河岸垂直）

作法：过点B作BB'垂直于河岸，且使BB'长等于这条河宽，连接AB'交河的一岸于点C，过点C作CD垂直于河岸，与另一岸交点D,则CD即为架桥最合适的位置。

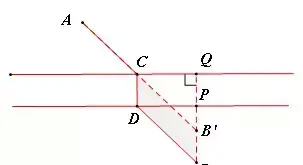
验证：在河的两岸任取一点C',D'，连接B'C'，易知四边形BB'C'D'是平行四边形，则AC'+C'D'+BD'=AC'+B'C'+BB'>AB'+BB'=AC+CD+DB（三角形的两边之和大于第三边）

【例7】(难度系数☆☆☆)如图，在平面直角坐标中，已知点A（0，2）、B（4，0），点C、D分别在直线x=1与x=2上，且CD∥x轴，则AC+CD+DB的最小值为______．

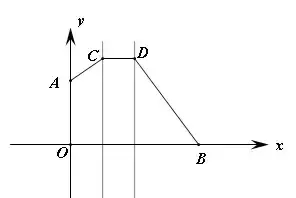
【分析】这是典型的架桥问题，将B沿x轴向左平移一个单位到B’，连接AB'，交直线x=1于点C，交直线x=2于点D，此时AC+CD+DB的值最小，最小值为AB'+CD=√13+1.

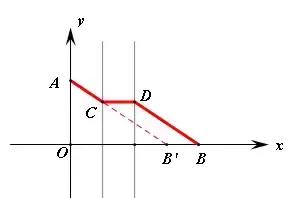
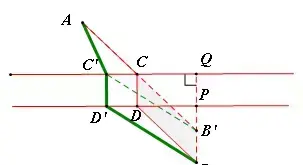
【例8】(难度系数☆☆☆)如图，A、B是直线a同側的两定点，定长线段PQ在a上平行移动，问PQ移动到什么位置时，AP+PQ+QB的长最短？

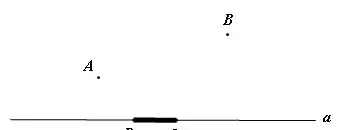
【分析】本题与架桥问题有所区别，动线段不是在平行线间移动了，而是在一条直线上移动，故处理策略截然不同，需用轴对称及平行四边形的性质化折为直。作AA'平行且等于PQ，再作A'关于直线a的对称点A''，连接A''B，与直线a的交点为D，在D的左边截取线段CD，使CD=PQ,则当PQ移动到与CD重合的位置时，AP+PQ+QB的长最短。

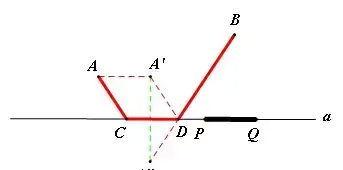
类型五：三动型

【模型介绍】在直角△ABC中，∠B=90°，D,E,F分别是边AB,BC,CA上的点，求DE+EF+DF的最小值。

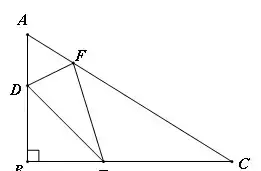
分析：首先假设F点固定，作关于AB,BC的对称点F',F''（如图1），则DE+EF+FD=DE+F'D+F''E，此时最小值就是线段F'F''的长。于是问题转化为：当F运动时，F'F''什么时候最短。将Rt△ABC补全为菱形（如图2），发现F‘，F''是这个菱形对边上的关于B中心对称的对称点，很容易发现，F'F''的最短距离就是菱形对边的距离，即菱形的高。此时（如图3）F就是斜边AC上的高的垂足点，D,E与B点重合。

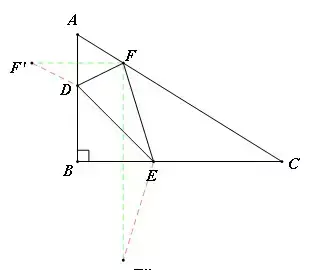
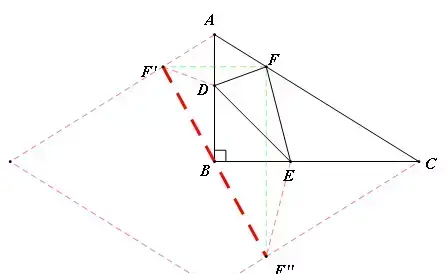
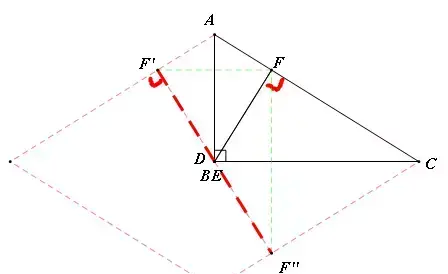
验证：如图所示，在AB,BC上任取点D,E，则FD+DE+EF=F'D+DE+EF''>F'F''(两点之间线段最短)

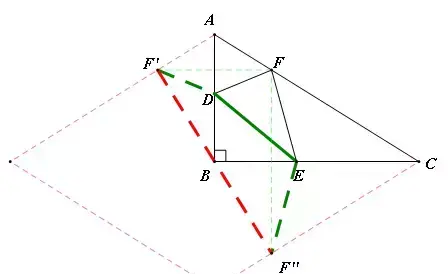
【例9】(难度系数☆☆☆☆)在直角△ABC中，∠B=90°，D,E,F分别是边AB,BC,CA上的点，AB=3,BC=4,求DE+EF+DF的最小值。

【答案】构造菱形，其对边间距离为4.8，即DE+EF+DF的最小值为4.8

【总结】两定一动型是较为简单的一种类型，其要领是作一定点关于动点所在直线的对称点，若题目是以几何图形（如正方形、菱形、等边三角形等）为背景，则应利用图形自身的轴对称性来找它的对称点。而其他模型大多以此模型为基本方法，利用轴对称或平移变换化折为直，由此可见，转化思想是解决此类问题的基本思想。

最短路径有技巧

五类模型含架桥

平移旋转与对称

化折为直本领高

温馨提示：通过以上关于「初中数学」利用轴对称解决常规的线段和最值问题内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。