整数拆分问题(整数的分拆解题方法)

小学数学思维训练——第七讲 整数的分拆

整数分拆是数论中一个既古老又活跃的问题.把自然数n分成为不计顺序的若干个自然数之和

　　n=n1+n2+…＋nm（n1≥n2≥…≥nm≥1）的一种表示法，叫做n的一种分拆.对被加项及项数m加以一些限制条件，就得到某种特殊类型的分拆.早在中世纪，就有关于特殊的整数分拆问题的研究.1742年德国的哥德巴赫提出“每个不小于6的偶数都可以写成两个奇质数的和”，这就是著名的哥德巴赫猜想，中国数学家陈景润在研究中取得了突出的成果.下面我们通过一些例题，简单介绍有关整数分拆的基本知识.

一、整数分拆中的计数问题

　　例1 有多少种方法可以把6表示为若干个自然数之和？

　　解：根据分拆的项数分别讨论如下：

　　①把6分拆成一个自然数之和只有1种方式；

　　②把6分拆成两个自然数之和有3种方式

　　6=5+1=4+2=3+3；

　　③把6分拆成3个自然数之和有3种方式

　　6=4+1+1=3+2+1=2+2+2；

　　④把6分拆成4个自然数之和有2种方式

　　6＝3＋1＋1＋1=2+2+1+1；

　　⑤把6分拆成5个自然数之和只有1种方式

　　6=2+1+1＋1＋1；

　　⑥把6分拆成6个自然数之和只有1种方式

　　6＝1+1+1+1+1+1.因此，把6分拆成若干个自然数之和共有

　　1+3+3＋2+1+1=11种不同的方法.

　　说明：本例是不加限制条件的分拆，称为无限制分拆，它是一类重要的分拆.

　　例2 有多少种方法可以把1994表示为两个自然数之和？

　　解法1：采用有限穷举法并考虑到加法交换律：

　　1994=1993+1=1＋1993

　　=1992+2=2＋1992

　　=…

　　=998＋996=996+998

　　=997+997

　　因此，一共有997种方法可以把1994写成两个自然数之和.

二、整数分拆中的最值问题

　　在国内外的数学竞赛试题中经常出现与整数分拆有关的最大值或最小值的问题.

　　例5 试把14分拆为两个自然数之和，使它们的乘积最大.

　　解：由例2可知，把14分拆成两个自然数之和，共有7种不同的方式.对每一种分拆计算相应的乘积：

　　14=1＋13，1×13＝13；

　　14=2+12，2×12=24；

　　14=3＋11，3×11=33；

　　14=4＋10，4×10=40；

　　14=5＋9，5×9=45；

　　14=6+8，6×8=48；

　　14=7+7，7×7=49.

　　因此，当把14分拆为两个7之和的时候，乘积（7×7=49）最大.

　　说明：本例可以推广为一般性结论：“把自然数n≥2分拆为两个自然数a与b（a≥b）之和，使其积a×b取最大值的条件是a=b或a-b=1（a＞b）”.事实上，假设a-b=1＋m（其中m是一个自然数），显然n=a＋b=（a-1）+（b＋1），而有（a-1）×（b＋1）＝a×b＋a-b-1＝a×b＋m＞a×b.

下面我们再研究一个难度更大的拆数问题.

　　问题：给定一个自然数N，把它拆成若干个自然数的和，使它们的积最大.

　　这个问题与前面研究的两个拆数问题的不同点是：问题中没有规定把N拆成几个自然数的和.这也正是这题的难点，使分拆的种类要增加许多.我们仍旧走实验-观察-归纳结论这条路.先选择较小的自然数5开始实验.并把数据列表以便比较.

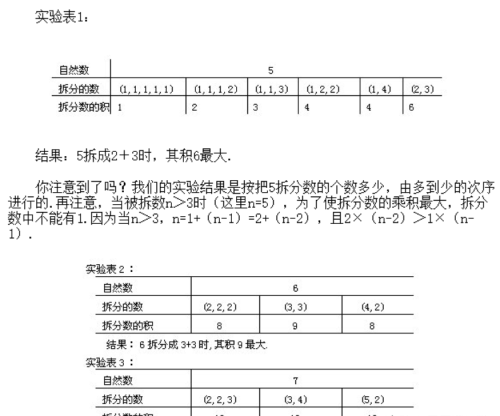
结果：7拆分成2＋2+3时.其积12最大.

　　注意，分拆数中有4时，总可把4再分拆成2与2之和而不改变分拆的乘积.

　　实验结果4：8拆分成2＋3+3时，其积最大.

　　实验结果5：9拆分成3+3+3时，其积最大.

　　实验结果6：10拆分成3+3+2＋2时，其积最大.

　　观察分析实验结果，要使拆分数的乘积最大，拆分数都由2与3组成，其形式有三种：

　　①自然数=（若干个3的和）；

　　②自然数=（若干个3的和）+2；

　　③自然数=（若干个3的和）+2＋2.

　　因此，我们得到结论：把一个自然数N拆分成若干个自然数的和，只有当这些分拆数由2或3组成，其中2最多为2个时，这些分拆数的乘积最大.（因为2+2+2=3+3，2×2×2＜3×3，所以分拆数中2的个数不能多于2个.）

我们以上采用的“实验-观察-归纳总结”方法，在数学上叫做不完全归纳法.我国著名数学家华罗庚讲过：难处不在于有了公式去证明，而在于没有公式之前怎么去找出公式.不完全归纳法正是人们寻找公式的重要方法之一.但是这种方法得出的结论有时会不正确，所以所得结论还需要严格证明.这一步工作要等到学习了中学的课程才能进行.

温馨提示：通过以上关于小学数学思维训练——第七讲 整数的分拆内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。