肖特基二极管15819(肖特基二极管10A)

肖特基二极管（1）

一，肖特基二极管

现在说起二极管，我们大多默认它是由“PN结”组成的；然而有一种奇特的、应用非常广泛的二极管，却并非由PN结组成，而是金属-半导体结构：肖特基二极管（SBD）。

最早接触硬件设计时，听说了肖特基二极管的大名，觉得这个二极管名字：陌生又顺口，似乎不是以其功能命名的，非常古怪。后来才知道肖特基二极管是以其发明人华特.肖特基博士名字命名的，我想这是流传百世的一个好办法，虽然跟桃花潭塘主：汪伦比还是差了一截。

肖特基二极管是以贵金属（金、银、铝、铂等）为正极，N型半导体为负极，利用二者接触面形成肖特基势垒，具有整流特性而制成金属-半导体器件。

我们来看下PN结的扩散理论：从“自由电子”高浓度的N区向低浓度的P区扩散“自由电子”，同理“空穴”浓度高的P区向N区扩散“空穴”；这非常容易理解，因为这符合日常观测经验，举个例子：在一瓶水中滴“墨水”，就能看到“墨水”不停扩散开，直至整瓶水的“墨水”浓度均匀分布。但套用到肖特基二极管，前提必然是：金属中的“自由电子”要远少于N区中的“自由电子”；这就不符合我们的常识了，N半导体的“自由电子”比金属导体中导电率最高的银的“自由电子”还要多？打死我都不信。

事实上，扩散理论已经不能应用在肖特基二极管上了，而需要用到“能带理论”来解释。我们会在接下来的“肖特基二极管的原理”章节进行解释；现在先放一放，先看相对更容易且重要的部分：肖特基二极管的结构。

1，肖特基二极管结构

肖特基二极管整体上是由金属和N半导体组成，但在实际结构比想象中更加复杂一些：

1. 阳极：由金属（金、银、铝、钼等材料）组成，用SiQ2来消除边缘区域电场，提高二极管反向耐压值；

2. 阴极：由N-外延层（低掺杂），N型基片（小通态电阻，掺杂浓度为N-的100倍），N+阴极层（减小阴极接触电阻）以及阴极金属组成；

3. 通过调整结构参数，在基片和阳极金属之间形成合适的肖特基势垒。

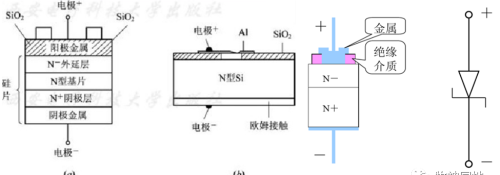
为什么肖特基势垒区的N半导体的掺杂浓度要低一些，而与阴极金属接触的N半导体掺杂浓度要更高呢？

1. 虽然还没讲到：为什么N区会失去电子而金属反而能得到电子；但事实就是：肖特基二极管中的金属替代了原来P型半导体，与N半导体之间建立了肖特基势垒，而且内建电场的方向是N半导体—>金属；

2. 参考PN结能带图，如果N区的掺杂浓度变大，那么肖特基势垒区间距就变小（由于金属不存在空穴，从N区跨越到金属的“自由电子”在金属表层，所以肖特基二极管势垒区只存在N区中，间距远小于PN结）；

——根据 “隧穿效应”原理：如果势垒区很小，那么在加反向电压时，金属侧“自由电子”能很容易的“隧穿”到N区，形成电流。

3. 高浓度掺杂的N区与金属的“接触电阻”就会便非常小（下面欧姆接触具体原理分析），这也解释了：为什么与阴极金属接触的N区是高掺杂的；

4. 如果N区的掺杂浓度很小，肖特基势垒区宽度足够大，就能够增加肖特基反向耐压；但肖特基势垒区天生比PN结距离要小，所以其反向电流会相对更大，反向耐压会更小。

肖特基二极管主要有两种工艺结构：点接触结构和平面接触结构；

1. 点接触：用一根尖端细金属丝与半导体接触制成，用机械接触或用放电工艺得到一个很小的合金结；

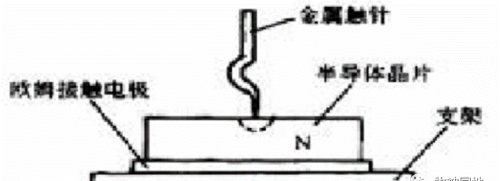
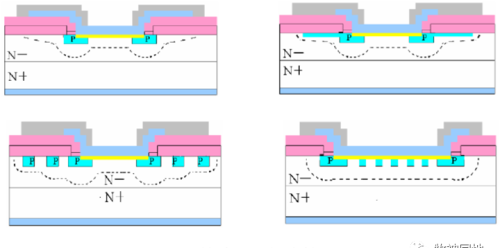
2. 平面结构是我们最常用的，它有很多不同的结构用于改进反向电压：

1, 平面结构比点接触的正向压降低，电流大，反向击穿电压有所提高；但是势垒结边缘电场集中，反向漏电流更大；VRM<60V；

2, 为了缓和边缘电场集中问题，采用了金属场板结构；

3, 为进一步改进边缘电场，增加P型保护环结构。

2，肖特基二极管原理

上面我们了解了肖特基二极管的基本物理结构，肖特基势垒结构和金属电极-半导体接触的结构并无本质差别，那只要是金属和半导体接触就会形成“肖特基势垒”么？接下来我们就可以看下：金属和N半导体怎么形成的“肖特基势垒”。

在深入之前，我们再来捋一遍肖特基势垒形成的基本原理：

1. N型半导体与金属接触时，半导体中的“自由电子”进入金属（不是扩散运动）；

2. N型半导体界面电荷区中留下正电荷--“空穴”，金属界面上有多余负电荷--“自由电子”，从而产生由N->金属的电场；

3. 由于金属内部“自由电子”在内建电场的作用下，产生金属->N的漂移运动，并最终达到平衡，形成肖特基势垒，如下图所示。

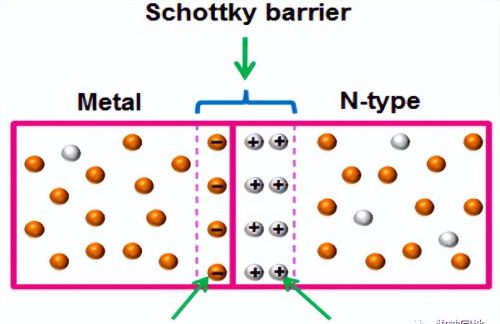
很明显，除了第一步外，其它两个步骤都很好理解。所以我们需要引入新的概念来解释为什么“自由电子”会从N半导体“扩散”到金属呢？

1. 金属功函数：金属由金属内部逸出到表面外的真空所需要的最小能量；即：φm = E0-(EF)m；E0为真空电子能量（真空能级），(EF)m为金属费米能级；

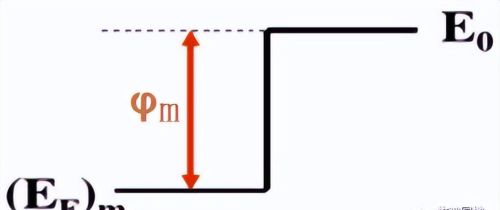
1, “金属键”的约束力很弱，“自由电子”可以在金属内部是自由移动；

2, 但金属功函数要求的是：“自由电子”突破金属原子核的电磁力，逸出到金属外面的能量，这显然是需要更大的能量。

2. 同理，半导体功函数是指：E0与半导体费米能级之差，φs = E0–(EF)s；但半导体费米能级下的价电子有概率会跃迁到导带上，变成“自由电子”；所以有了另外一个概念：半导体电子亲和能，即：半导体“导带底”的“自由电子”逸出体外所需的最小能量，χ= E0–Ec；

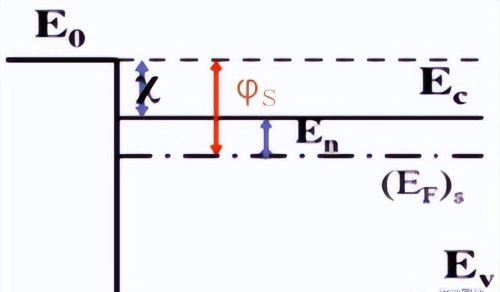
好啦，那接下来就要比一比“金属功函数”和“半导体电子亲和能”谁大，谁小的问题了：

1. 金属或半导体中的“自由电子”想要进入对方材料中，那么金属中“自由电子”需要克服“金属功函数”；

2. 而N半导体“自由电子”则需要克服半导体亲和能。

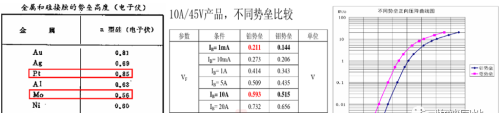
如下图所示为几种常用金属的功函数和半导体材料的电子亲和能值。我们可以看到，金属的功函数居然大于半导体的电子亲和能，说明半导体中的“自由电子”有更大的概率（更容易）逸出并进入金属，相反金属中的“自由电子”逸出并进入半导体的概率要小。这就解释了为什么“自由电子”是从半导体到金属的方向移动。

从上图可以看到，不同金属的功函数以及不同半导体的电子亲和能有差别，所以不同的金属与半导体形成的势垒高度也会不同，从而导致肖特基二极管V-I曲线的差异，如下图所示：如果金属接触势垒高度高，那么二极管漏电流小，正向导通压降大。

还有一个问题是：为什么PN结不用考虑电子亲和能，可以直接用扩散理论呢？

个人理解：因为P型半导体和N型半导体，它们虽然由于不同的掺杂导致“自由电子”和“空穴”的浓度差异，但是究其本质来说，P型和N型半导体就是同一种材料，所以“自由电子”和“空穴”进出P型或N型半导体不需要逸出本体（不需要做功，或则说P和N型的“半导体电子亲和能”是一样的）；要看谁进入对方更多，就看 “自由电子”或“空穴”的浓度，所以我们可以用“扩散理论”来解释PN结的扩散运动。

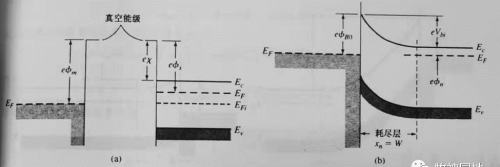
接下来，我们再来看下肖特基势垒的能带图；以真空能级E0作为参考能级，φm是金属功函数，φs是半导体功函数，χ是电子亲和能；如下图左所示，在金属和半导体接触之前：φm>φs。

1. 如下右图为理想热平衡状态时的金属-半导体能带图，由于接触前半导体的费米能级要高于金属的费米能级，接触热平衡之后两者费米能级必然保持连续，所以半导体中的“自由电子”流向比它能级更低的金属中，带正电的“空穴”仍然留在半导体中，从而形成一个空间电荷区（耗尽层）；

2. φB0是半导体接触的理想势垒高度，金属中的“自由电子”向半导体中移动形成势垒，该势垒就是：肖特基势垒；φB0= φm - χ；

3. 在另外一侧，Vbi是内建电势差，这个势垒类似于PN结势垒，是由导带中电子运动到金属中形成的势垒；Vbi = φB0- φn；

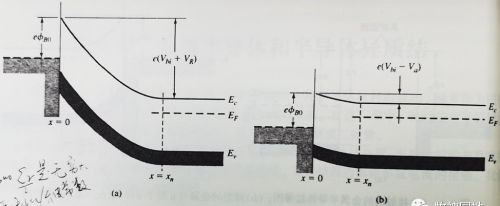
如下图分别为肖特基二极管的反偏和正偏能带图，与PN结能带图非常类似；

1. 在金属与半导体之间加一个负电压，那么半导体-导体势垒高度会增大，理想情况下φB0保持不变，但金属与半导体之间内建电势差增大，这种情况是反偏；

2. 如果在金属和半导体之间加一个正电压，φB0依然保持不变，而半导体金属势垒高度会减小，“自由电子”很容易从半导体流向金属，这种情况是正偏。

3. 肖特基二极管施加电压后的金属-半导体能带图与PN结非常类似，其电流主要取决于“自由电子”的流动，正偏电流方向是从金属流向半导体，电流是随正偏电压Va的指数函数。

温馨提示：通过以上关于肖特基二极管（1）内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。