向量场的线积分(向量微积分和多元微积分)
五分钟MIT公开课-多元微积分:向量场和线积分
简介
这期的内容要先把二重积分放一边了,开始一段相对较新的内容。
虽然是新内容,但是却是生活中很常见的现象,向量场的应用非常广泛,我们所生活的空间,也是在一个巨大的向量场中。
MIT多元微积分的系列课程中,在微分的部分就已经接触过向量场了,但是并没有做特别的申明。通过向量场,给一个重要的问题提供了非常有意思的思考角度——拉格朗日算法的几何学描述。具体可看:
五分钟MIT公开课-多元微积分:拉格朗日乘数法
目录:
简介
向量场
功和线积分
几何法
向量场向量场就是向量构成的一种形式。分量M和N是关于位置x,y的函数。
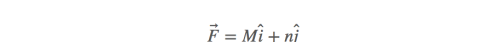
平面上的每个点都有对应的向量。向量场的例子也很普遍,比如说这是一张风向图,向量场存在于每一点处。而向量都依赖于点的位置:
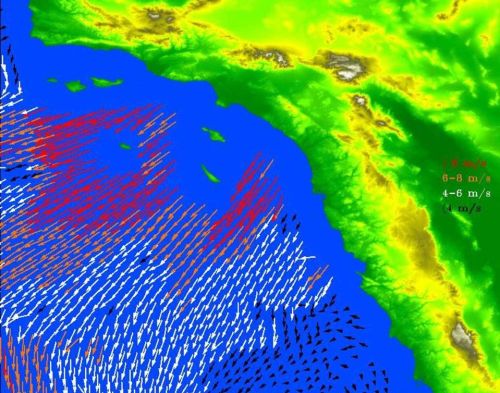
还有一个更加直觉的例子就是地球的重力场,无论在哪里放置一个物体,这个物体都会受到向下的重力。
现在要从数学的角度去理解向量场,所以可以不用关心这些向量具体是什么。
要研究向量场,首先要知道怎么画出这些向量。
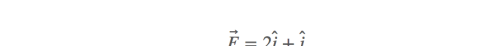
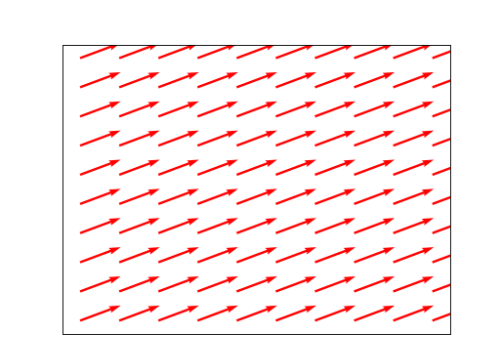
注意可能会混淆的地方,向量坐标和位置坐标是不同的,在这个例子中不同的位置有同样的向量。
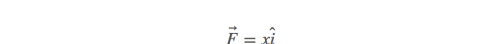
j分量为0,只有i分量,向量场是水平的。关键是要知道这些向量的长度是多少。长度取决于x:
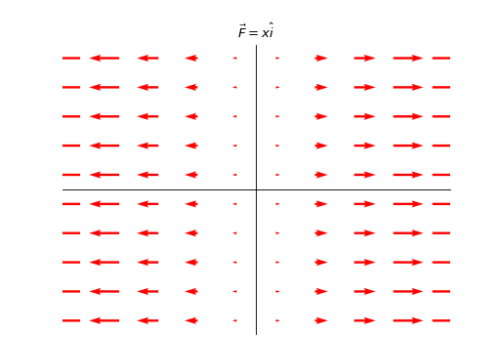

这个向量场是从原点放射状的向量,随着距离原点的距离增大而增大。
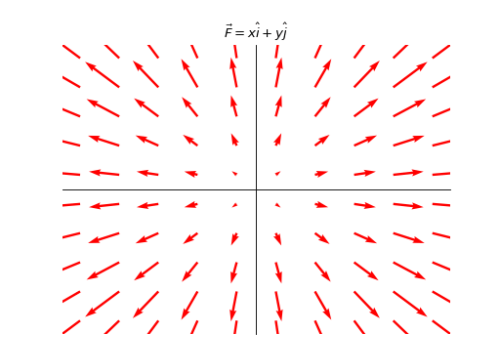
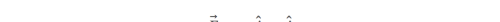
在每个点(x,y)处的向量是(-y,x),相当于位置向量逆时针旋转90度。离远点越远,向量越大。这与流体运动时,绕着某点匀速转动时形成的向量场一致。这就是匀速转动的速度场,并且各点绕原点一圈的时间是2pi。
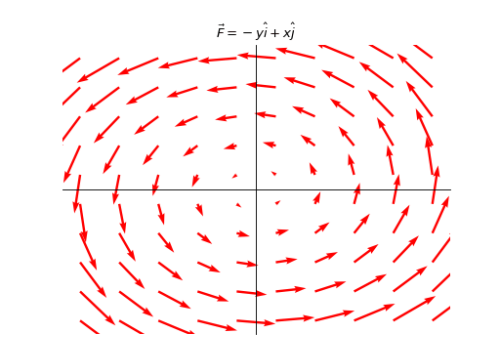
知道向量场后有很多东西可以学习,现在从力对物体做得功为突破口来深入了解向量场。
功和线积分考虑某个位置上有一个力,如果某个质点受到外力的作用,质点的运动就会形成轨迹。外力所做的功就等于外力与位移向量的点积。但是,如果质点的运动轨迹非常复杂或者外力不是恒力,这时就需要做积分了。这就是线积分。
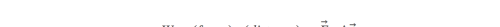
向量\Delta r 表示的是位移,是位置向量的改变量。
功的计算是将移动路径分成许多小段,每一小段都有一个与之对应的向量,并求出每个向量与对应外力的点积,在把所有点积加起来。
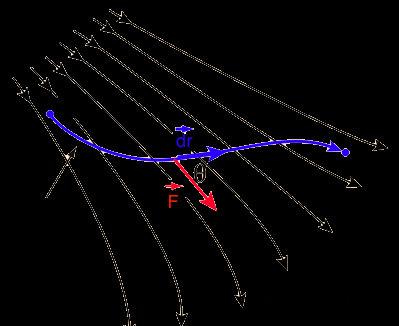
沿着某条轨迹C,外力所做的功等于其积分。表示为:沿着轨迹C,F与dr的点积的积分:
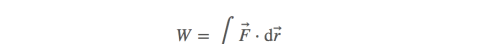
可以这样去想,这是一个极限,我们把轨迹切割成非常小的线段,求出所有给定点的点积之和:
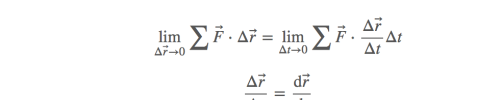
所以原式:
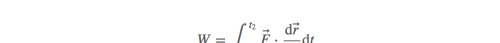
例子
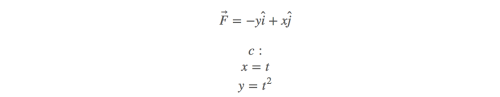
这个向量场让所有的点绕原点旋转。

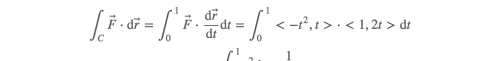
几点思考:
为什么不直接使用dr?
因为dr不是常规变量,很难处理,这里只把它当作符号就好了。向量r不是标量,而是位置向量,所以不能求F对于r对积分,因为无法对向量求积分。
如果质点从A到B沿着其他路径,力做功是否相同?
肯定是不相同的,假设在x轴上有一点c,从原点到c力是不做功的,从c到b明显力做功和原点到b所做功不同。考虑线积分的定义,线积分的值,取决于从a到b的路径。这就是为什么要使用曲线的参数方程。外力做功与路径有关。
如果外力作用导致的质点轨迹改变,力做功如何计算?
这就需要解微分方程了,从微分方程中可知质点的运动轨迹。
另一个角度来思考
F有两个分量,dr也有两个分量:
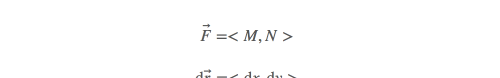
注意后者虽然形似向量,却不是真正的向量。这样线积分的方程就可以写成这样:
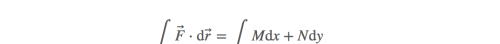
现在已经不是向量场而是微分运算了,但是他们的本质是相同的,所以关键在于如何计算这个积分。对于这个积分,M和N都依赖于x和y,如果仅对其中一个求积分,那么另一个就不能够被消掉。难点在于x和y互相关联。那么有人就会想到使用变量转换,但是无论怎么变换肯定会存在两个变量。实际上,曲线c只有一个参数,最终我们希望只剩下一个变量,这样就成为求单变量积分的问题了。解决的办法是:把x和y写成含有同一个变量的式子,然后用这个变量替换x和y。
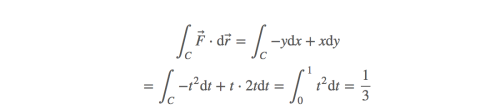
注意:
线积分只取决于轨迹C,跟如何参数化无关。所以只要能简化成任何一个参数都行,比如使用极坐标。
几何法首先来看看向量dr的含义。什么是向量 dr,什么是向量 \Delta r?
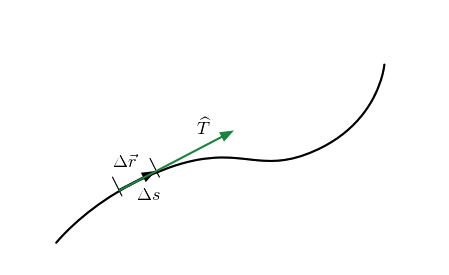
在轨迹上取非常小的一段,\Delta r 的方向就是向量的方向,它与单位切向量 T 有相同的方向。\Delta r 的长度就是就是轨迹上的弧长,记为 \Delta s。这个向量方向沿着切线方向,大小为轨迹的弧长。
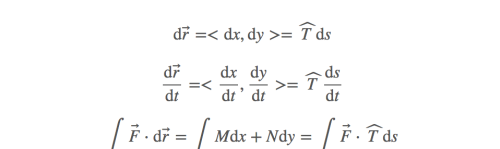
F和T的点积是一个标量,几何上表示外力投影到轨迹切线方向的成分,然后求出这个成分在曲线上的积分。结果是一样的,但是这种思考方法会让问题变得简单。
回顾上一个例子,使用几何法,对每一小段轨迹所受力在切线方向的投影总和,与积分得到的结果非常近似。

例子
轨迹是以原点为圆心a为半径的圆,逆时针旋转,向量场为:

对于这个例子,采用几何法,在轨迹上任意一点,外力恒垂直于运动方向,所以做功为0。
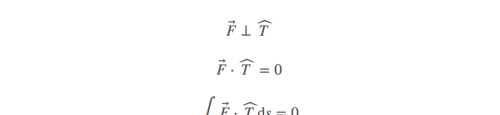

现在考虑,轨迹不变,向量场为:

这时,F与切线方向相同

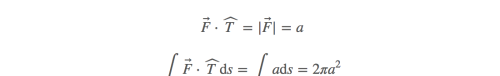
总结
线积分的三种思考方式:
单变量的向量积
多变量的微分
几何法
温馨提示:通过以上关于五分钟MIT公开课-多元微积分:向量场和线积分内容介绍后,相信大家有新的了解,更希望可以对你有所帮助。