不怕不成功,就怕你根本不尝试(不怕什么就怕不努力)

压轴题不可怕，就怕你不够努力

考生最怕中考哪门科目？

我想如果对所有中考考试科目进行排名，数学肯定是排在第一位。数学这门科目因其具有逻辑性和抽象性等鲜明特点，让很多学生一直找不到学习门路，更别说考出一个优秀的分数。因此，如何提高数学学习效率和学习成绩，成为了很多老师、家长和学生非常关心的话题。

提到中考数学，那我们就不得不提最后两道综合题，也就是平常所说的压轴题。

什么是压轴题？就是那些具有综合性强、解法灵活多样、知识点丰富等特点的题型，此类题目能很好考查考生分析问题和解决问题的能力，如动点问题就是非常具有代表性的一类问题。

什么是动点问题？

一般是指图形中存在一个或多个动点，它们是在某条线段、射线或弧线上运动的，从而引起另一图形的变化，从运动变化的角度来研究、探索发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理，是一类开放性题目。

动点问题对考生的观察能力和创新能力要求较高，题目的难度一般比较大，是全国各省市中考数学试题的热点题型。

动点问题之所以会难，主要在于它能把很多知识内容结合在一起，形成不同类型的动点综合问题，如函数动点综合问题、代数动点综合问题、函数与几何动点综合问题、几何动点综合问题等。

动点问题有关的中考试题讲解分析，典型例题1：

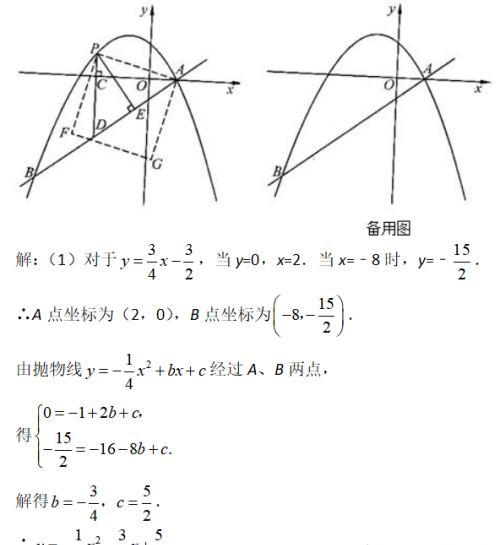
如图，在平面直角坐标系中，直线y=3x/4-3/2与抛物线y=-x²/4+bx+c交于A、B两点，点A在x轴上，点B的横坐标为﹣8．

（1）求该抛物线的解析式；

（2）点P是直线AB上方　 　的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E．

①设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的最大值；

②连接PA，以PA为边作图示一侧的正方形APFG．随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标．

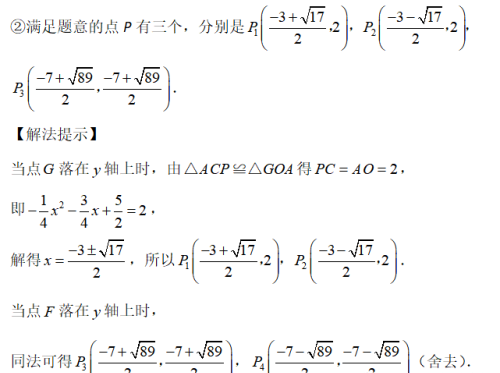
考点分析：

二次函数综合题

题干分析：

（1）利用待定系数法求出b，c即可；

（2）①根据△AOM∽△PED，得出DE：PE：PD=3：4：5，再求出PD=yP﹣yD求出二函数最值即可；

②当点G落在y轴上时，由△ACP≌△GOA得PC=AO=2，解得x，

所以得到p₁和p₂的坐标，当点F落在y轴上时，同法可得p3和p4的坐标（舍去）．

解题反思：

此题主要考查了二次函数的综合应用以及相似三角形的判定以及待定系数法求二次函数解析式，利用数形结合进行分析以及灵活应用相似三角形的判定是解决问题的关键．

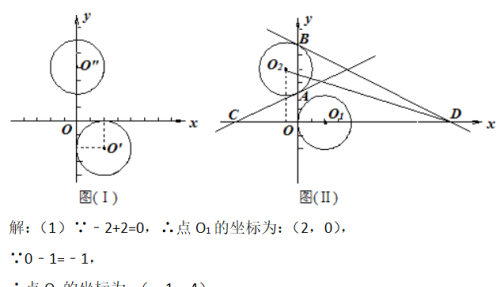
动点问题有关的中考试题讲解分析，典型例题2：

如图（Ⅰ），在平面直角坐标系中，⊙O′是以点O′（2，﹣2）为圆心，半径为2的圆，⊙O″是以点O″（0，4）为圆心，半径为2的圆．

（1）将⊙O′竖直向上平移2个单位，得到⊙O₁，将⊙O″水平向左平移1个单位，得到⊙O2如图（Ⅱ），分别求出⊙O₁和⊙O₂的圆心坐标．

（2）两圆平移后，⊙O₂与y轴交于A、B两点，过A、B两点分别作⊙O₂的切线，交x轴与C、D两点，求△O₂AC和△O₂BD的面积．

考点分析：

切线的性质；坐标与图形变化-平移；综合题。

题干分析：

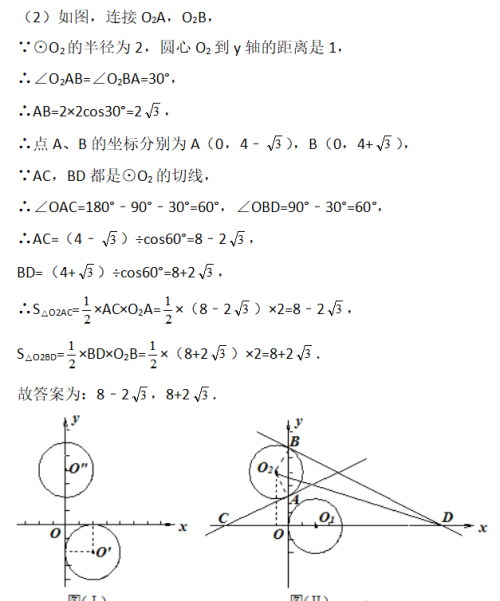
（1）根据“左减右加，下减上加”的规律对点O′，O″的坐标进行平移即可得到点O1，O2的坐标；

（2）先求出点A、B的坐标，然后连接O2A，O2B，根据直角三角形30度角所对的直角边等于斜边的一半得出∠O2AB=∠O2BA=30°，又AC与BD是圆的切线，然后求出∠OAC=∠OBD=60°，利用特殊角的三角函数与点A，B的坐标即可求出AC、BD的长，最后代入三角形的面积公式进行计算即可．

解题反思：

本题主要考查了切线的性质与坐标的平移，利用数据的特点求出30度角是解题的关键，也是解答本题的难点与突破口，本题难度适中，有一定的综合性．

动点问题都是以运动的点、线段、变化的角、图形的面积为基本条件，给出一个或多个变量，要求确定变量与其他量之间的函数等其他关系；或变量在一定条件为定值时，进行相关的计算和综合解答，解答这类题目，一般要根据点的运动和图形的变化过程，对其不同情况进行分类求解。

温馨提示：通过以上关于压轴题不可怕，就怕你不够努力内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。