mit多变量微积分笔记(多变量微积分公式)

五分钟MIT公开课-多元微积分：变量转换

简介

关于变量的转换其实在之前的知识中已经有一些接触了，请参考

五分钟MIT公开课-多元微积分：极坐标的二重积分

关于二重积分的知识可以回顾：

五分钟MIT公开课-多元微积分：二重积分

五分钟MIT公开课-多元微积分：二重积分的应用

这一节是对这一问题更深入的探讨。

知道如何在直角坐标系中处理二重积分，也知道直角坐标系和极坐标系的互相转换，一般情况下，变量转换更加普遍。这一节讲如何在二重积分下做变量变换。

热身：计算椭圆的面积

计算一个以a，b为半轴的椭圆面积。

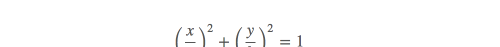
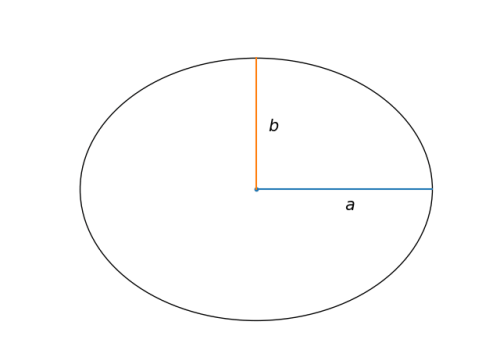
可以在直角坐标系下求面积，但是我们发现并不容易。椭圆是一个被压扁的的圆，直接使用极坐标也不方便。所以首先，要简化：

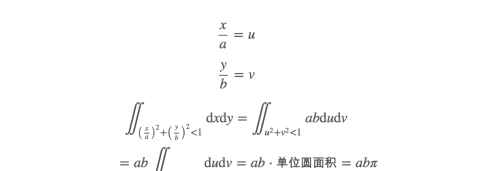
椭圆的参数变换后，是一个单位圆，这样椭圆的面积就好算了。

用变量替换的方法会使问题变得简单。

如果问题进一步复杂，就要使用更普遍的方法。关键问题是：比例因子（scaling factor）是什么？dxdy和dudv之间的关系是什么？

线性变换

例:

定义：

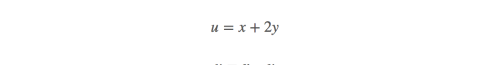
一般情况下，做线性变换的目的，不是简化积分就是简化积分限。（simplify the integrant or the bounds）

单位面积：

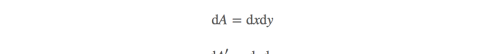
要明确的是，这种线性变换将所有的直线进行相同的变换，而且可以找到一个常比例因子（constant scaling factor）.变换的四边形并不会因为位置的改变而改变。

定义比例因子：不受位置选择的影响。因为这是对变量的线性变换。

如图所示，右边绿色平行四边形为变换后的区域。

平行四边形的面积可以通过行列式来求：

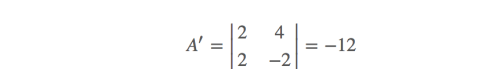
负号仅仅表示方向相反。

所以

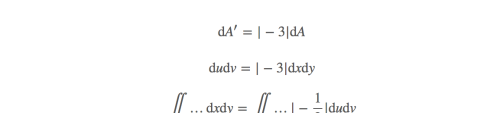
面积变为原来的三倍，方向相反了。

还有件事情要注意就是积分限也跟着变化了。

定义：

通常情况：

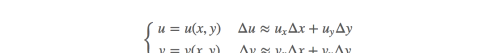
使用矩阵表达：

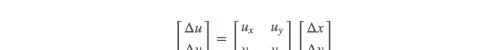
当进行线性变换的时候，变换矩阵的行列式代表缩放面积系数。（可以带入验证）

变量替换的雅可比矩阵（Jocabian）表示

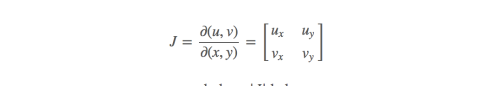
注意这里没有真的在求偏导数，只是表示dudv和dxdy之间有比例关系的表达方式。

例子：极坐标

回顾直角坐标系到极坐标系的变化就是将 dxdy 变化为rdr d theta。现在用新的知识来解释下到极坐标的变换。

已知变换公式为：

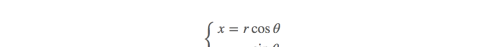
极坐标变换的雅可比矩阵的行列式为：

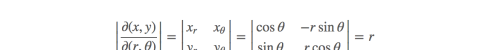
所以：

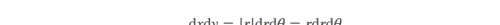
补充：

如果计算从xy到uv的雅可比变换矩阵，这个矩阵和uv到xy的变换矩阵互为倒数。

压轴：一个完整的例子：

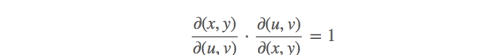
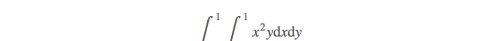
如果不通过变量变换，这是一道很简单的题目。现在强行进行一组变量变换。

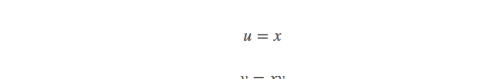
第一步：找到单位面积元

通过雅可比，

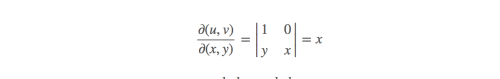
第二步：得到被积函数

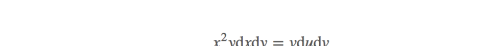
第三步：确定积分区间

这一步是最难的，这里给两种思考方案：

方案一：在xy域上找区间

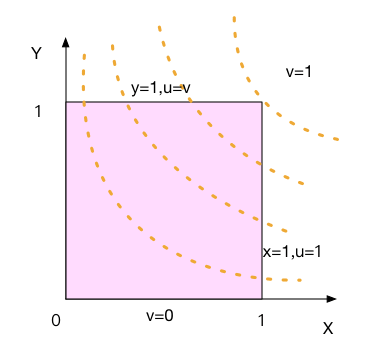
先看内积分的取值范围，即u的取值范围，先将v看做定值。黄线是v取不同值时的函数轨迹，我们关心的是这些黄线在什么时候进入XY的区域，什么时候离开，这就是u的积分空间。很明显，在y=1时，有u=v，在x=1时，有u=1。得到u的积分区间为[v,1]。

在看外积分的取值范围，xy最小值为0，最大值在XY区间的右上角，为1。所以v的积分区间为[0,1].

方案二： 在uv域上找区间

把xy域上的所有边界都变化到uv上

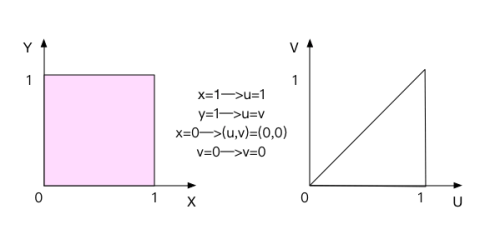
最后得到变换变量后的积分：

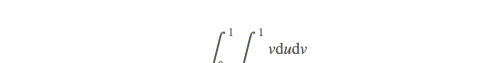
温馨提示：通过以上关于五分钟MIT公开课-多元微积分：变量转换内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。