求正三角形的边长公式(正三角形的边怎么求)

一道高中几何题-求正三角形的边长

已知等边三角形ABC中内有一个点P，且PA=8，PB=6，PC=10，求这个正三角形的边长。

解：

方法1：

如图所示的草图，其中将三角形APC顺时针转动60度，使得AC落在AB上，这样点P落在了点D，

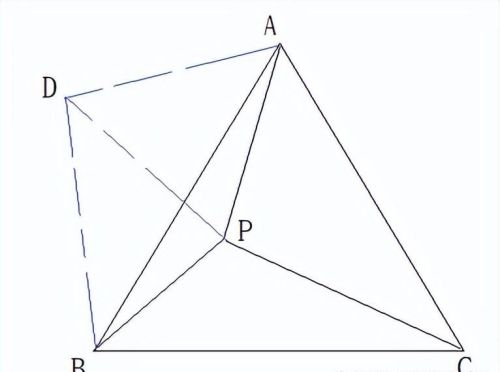
显然三角形APC全等于三角形ADB，这是因为

∠BAC=∠DAP=60°

因此∠DAB=∠PAC=60°-∠BAP

此外DA=PA， BA=CA，

根据SAS定理，证明得出三角形APC全等于三角形ADB。

所以DB=PC=10，

另外在三角形DAP中，因为∠DAP=60°，且DA=PA，所以该三角形是等边三角形。

所以DP=PA=8

这样三角形DBP是个6-8-10三个边形成的直角三角形（因为满足3-4-5的比例），

因此∠DPB=90°，

由此求出∠APB=90°+60°=150°

在三角形PAB中，利用余弦定理可以求出边AB，

由此得出：

方法2：利用解析几何，建立坐标，

如图所示，设等边三角形的边长为s, 将C置于原点，

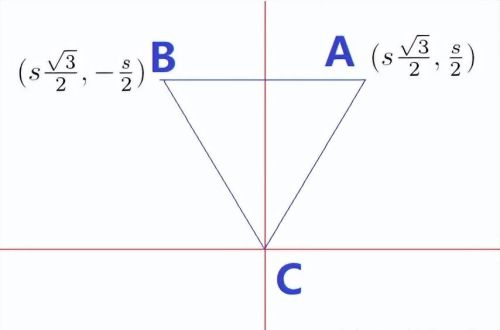
设点P为（x, y）, 根据已知列出三个方程：

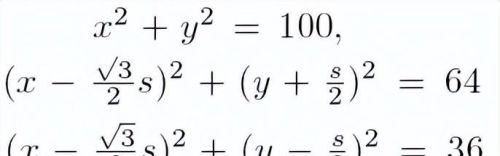
消掉x, y得出：

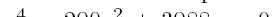
由此得出：

最后得出

温馨提示：通过以上关于一道高中几何题-求正三角形的边长内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。