简述加速度的切向分量和法向分量对物体运动的影响(切向加速度分量表达式)
「TNB标架;加速度的切向分量和法向分量」图解高等数学-下 08

笛卡尔坐标系对于描述运动的向量并非最合适的, 使用 TNB 标架来解释路径和沿路径运动的性质.T: 代表前进方向的单位切向量N: 代表路径弯曲方向的单位法向量B: 代表沿垂直与这两个向量确定的平面方向, 也就是从这个平面扭转出来趋势的次法向量, B = T x N .
三叶结,带有切线、法线和副法线沿曲线的动画:

每个运动体带着一个 TNB 标架运动, 该标架刻画了运动路径的几何特征. 比如 |dT/ds| 表明一辆车的路径向左向右弯曲程度, 称为车的路径的曲率;
-(dB/ds)·N 表明车的路径从运动平面扭转了多少, 称为车辆路径的挠率. 如上动图所示那样, 如果红点 P 是在弯曲公路上形式的汽车, 车灯的单位距离左右弯曲的变化率是公路的曲率, 而 T 和 N 确定的平面扭转的变化率是挠率.
空间曲线的曲率和法向量空间曲线的单位切向量 T 定义与平面曲线一样.
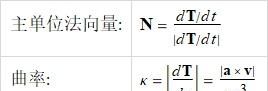

从上面的动画可以, 当固定 a 而增加 b 时, 曲率减少. 当固定 b 而减少 a 时, 曲率也会减小. 这表明拉伸弹簧就有把它弄直的趋势.
如果 b=0, 螺旋线退化为半径为 a 的圆, 则曲率为 1/a. 如果 a=0, 螺旋线退化为 z 轴, 曲率为 0. 观察下面动图:

空间的次法向量是 B = T x N, 也就是同时正交 T 和 N 的单位向量. T, N 和B 定义了一个右手向量标架, 这对于计算在空间中运动的质点的路径非常有意义.

曲率 κ 只能为正值, 但挠率可正可负, 也可以为 0.
由 T, N,B 确定的三个平面如下图所示. 曲率 κ = |dT/ds| 可以理解为点 P 沿曲线运动时候法平面(Normal Plane)转动的速率. 挠率 τ 是点 P 沿曲线运动时密切平面绕 T 转动的速率.

当物体运动时, 主要关注的是在运动方向即切方向 T 的加速度是怎样.

加速度总在正交于 B 的 T 和 N 的平面内, 并且能从上式中可以得知在正切方向产生了多少加速度, 在正交运动的方法产生多少加速度. 并且加速度是速度的变化率, 所以切向分量反映的 v 的长度的变化, 而法向分量测量 v 的方向的变化速率.

便于计算曲率和挠率的公式:
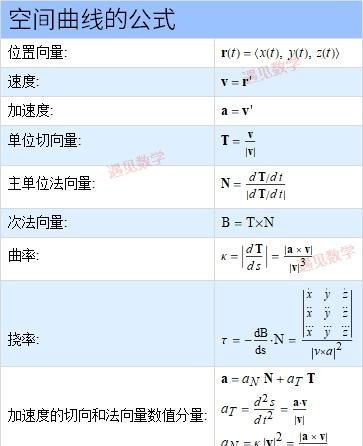
(完)
「予人玫瑰, 手留余香」
转发既是支持, 我们会努力走得更远!
温馨提示:通过以上关于「TNB标架;加速度的切向分量和法向分量」图解高等数学-下 08内容介绍后,相信大家有新的了解,更希望可以对你有所帮助。