两圆的切线长公式(求两圆的切线)

两道圆的切线中考题，等你来大显身手

【题目呈现】

1.如图，△ABC内接于⊙O，BD为⊙O的直径，BD与AC相交于点H，AC的延长线与过点B的直线交于点E，且∠A=∠EBC.

(1)求证:BE是⊙O的切线;

(2)已知CG∥EB，且CG与BD、BA分别相交于点F、G，若BG×BA=48，FG=√2，DF=2BF，求AH的值.

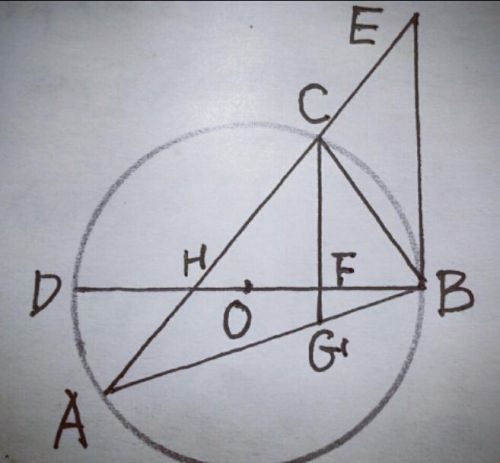
【分析】①，欲证BE是⊙O的切线，而DB是直径，须证∠EBD=90°即可，∵有条件∠A=∠EBC，因为证直角，须得找已有的或可证的直角，于是连接CD，如图，

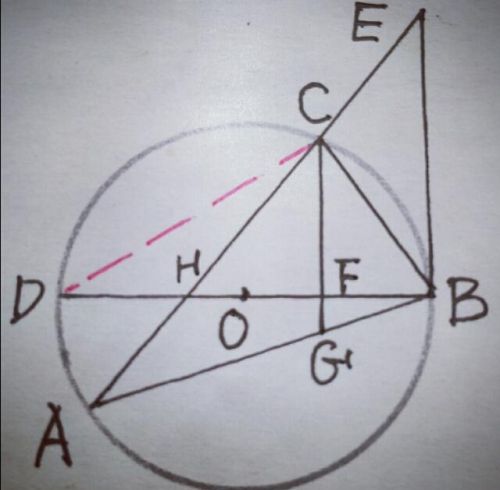
则∠A也转到∠D上，同时∠BCD=90°，∴∠D十∠CBD=90°，而∠D=∠A=∠EBC，∴可证∠EBD=90°，从而BE是⊙O的切线.

(2)注意到这样一个条件:BG×BA=48，出现乘积形式，想到相似的知识，有两个类似的模型，如图

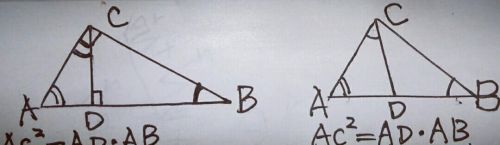
这两个图形，左边是射影定理模型，有人称它们为母子相似模型，都共用∠A，∠ACD=∠B，有着类似的结论(熟记后帮助解题),对照题中的条件，找相似三角形，∵CG∥EB，∴∠BCG=∠EBC，而∠A=∠EBC，∴∠A=∠BCG，又∠CBG=∠ABC，∴

△ABC∽△CBG，∴BC/BG=AB/BC，即BC²=BG×BA=48，∴BC=4√3，再看，∵CG∥EB，∴CF⊥BD，∴Rt△BFC∽Rt△BCD，∴BC²=BF×BD，又DF=2BF，∴BF=4，在Rt△BCF中，可得CF=4√2，∴CG=CF十FG=5√2.在Rt△BFG中，可得BG=3√2，又BG×BA=48，∴BA=8√2，∴AG=5√2，∴CG=AG，∴∠A=∠ACG=∠BCG，∵∠CFH=∠CFB=90°，∴∠CHF=∠CBF，∴CH=CB=4√3，而△ABC∽△CBG，∴AC/CG=BC/BG，∴AC=BC×CG/BG=20√3/3，∴AH=AC一CH=8√3/3.第2问抓住BG×BA=48这一突破口，层层推算，才能达到目的，若记不住上边的模型，此题也很难.

2.如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作⊙O的切线DE交AC于点E，AC的反向延长线交⊙O于点F.

(1)求证:DE⊥AC;

(2)若DE十EA=8，⊙O的半径为10，求AF的长度.

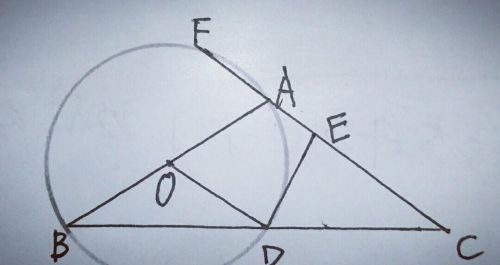
【分析】①要证DE⊥AC，已有DE是⊙O的切线，∴OD⊥DE，须证OD∥AC，须证∠ODB=∠C，而∠ODB=∠B，须证∠B=∠C，须证AB=AC(已知)，从而得证.

②要求AF的长，已知半径为10，AE十DE=8，显然要列方程，如何找等量关系？注意到∠ODE=∠DEA=90°，两个直角，再有一个直角即成矩形，于是过O作OH⊥AF，则OH平分AF，求出AH也可求出AF，并且OH=DE，HE=OD=10，如图

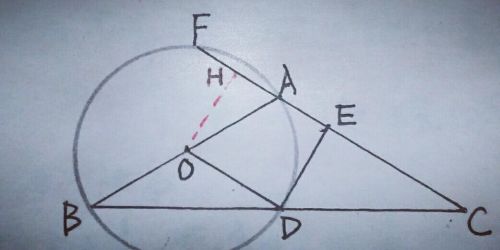
设AF=x，则AE=10一x，OH=DE=8一(10一x)=x一2.在Rt△AOH中，由勾股定理，知AH²十OH²=OA²，即x²十(x一2)²=10²，解得x1=8，x2=一6(不合题意，舍去)，∴AH=8，AF=2AH=16.

能否再找一种方法呢？我们看到AB是直径，若连接AD，则AD⊥BC，又AB=AC，∴D是BC的中点，而连接BF，则BF⊥AC，由(1)知DE⊥AC，∴BF∥DE，∴DE=BF/2，若求出DE，可知BF，在Rt△ABF中，可求AF，如图

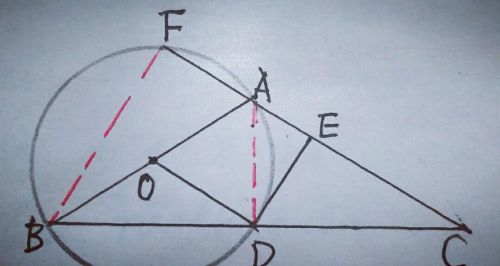
那么如何求DE呢？又知AC=AB=2×10=20，而∠ADC=90°，DE⊥AC，∠AED=90°，易知△AED∽△DEC，AE/DE=DE/EC，即DE²=AE×EC(射影定理)，设AE=x，则DE=8一x，EC=20一x，则(8一x)²=x(20一x)，解得x1=2，x2=16(不合题意，舍去)，∴DE=8一x=8一2=6，∴BF=12，在Rt△ABF中，由勾股定理，可得AF=16.

【总结反思】

与圓有关的线段的证明和计算，都具有很强的综合性，一般应用综合分析法，解题时需要从已知和求证两头出发，充分运用相关定理的基本图形的性质，架起已知和求证的"桥梁"，从而求得问题的解答.

感谢大家的关注、转发、点赞、交流！

温馨提示：通过以上关于两道圆的切线中考题，等你来大显身手内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。