勾股定理常见数组口诀(勾股定理的数字组)

一位高中数学教师眼中的“勾股定理”（续二） 勾股数组

几何学中有两件瑰宝，一是毕达哥拉斯定理，一是黄金分割律。前者我们可比之为黄金，后者我们可称之为贵重的宝石。

——开普勒

苏版教材八年级上册：勾股定理

定义：

一般地，若三角形三边长a，b，c都是正整数，且满足a，b的平方和等于c的平方，那么数组（a，b，c）称为勾股数组。勾股数组是人们为了解出满足勾股定理的不定方程的所有整数解而创造的概念。

直角三角形两直角边的平方和等于斜边的平方。如果用a、b和c分别表示直角三角形的两直角边和斜边，那么a^2+b^2=c^2。

常见基本勾股数组：

（3、4、5）， （5、12、13）， （7、24、25）；

（8、15、17）， （9、40、41）， （11、60、61）；

（12、35、37）， （13、84、85）， （15、112、113）；

（17、144、145）， （19、180、181）， （20、21、29）；

（20、99、101）， （48、55、73）， （60、91、109）。^

注：之所以叫基本勾股数组，是这些数组通过扩大n倍之后得到勾股数组没有归纳在内。

基本勾股数组的性质：

性质1

如果（a，b，c）是一个基本勾股数组，则此三数中的任意两个数都互质（这两个数的最大公约数是1）。

证明：

假设（a,b）有公约数m，即有a=ma1, b=mb1(m≠1) 于是，由c^2=a^2+b^2=m^2(a1^2+b1^2)

可知c也有约数m，因为（a，b，c）就不是基本勾股数组，与假设矛盾。

性质2

若是（a,b,c）基本勾股数组，则a,b不可能有相同的奇偶性，即为a,b为一奇一偶，而且c一定是奇数。

推广：对于所有的勾股数组（a,b,c）必有①a≠b;②a,b不能同时为奇数。

证明：

① 若a=b，则c=√2a不是整数，与假设相矛盾。

② 若a,b同时为奇数，设a=2m+1, b=2n+1,则c必是偶数，设c=2p,则c^2=4p^2，就是c^2一定被4整除。但是由c^2=a^2+b^2=4m^2+4m+1+4n^2+4n+1=4(m^2+n^2+m+n)+2,就是c^2被4整除，得到余数是2.也就是说c^2不能被4整除。这与上述结论矛盾。所以a,b不可能同时为奇数。

c语言:输出500以内所有勾股数

求法

下面的这种方法，可以找出无穷多个基本勾股数组（不一定是所有）。

写出数列I、II。

数列I由所有的自然数的平方数构成；数列II由数列I的相邻两数的差构成。只要在数列II中找出某个平方数，就可以求得一组勾股数组。如数列II中的第一个平方数是9=25-16，得到基本勾股数组（3,4,5）；第二平方数是25=169-144，得到基本勾股数组（5,12,13）.

数列II的通项公式为：（n+1）^2-n^2=2n+1,(n=1,2,3,…)

它是由除1之外的所有奇数构成，因此数列II中包含了除1外的所有奇数的平方数，它们依次是3^2，5^2，7^2，9^2…或9,25,49,81，…

为了使2n+1是除1之外的奇数的平方，n应有怎样的形式，由

2n+1=(2k+1)^2=4k^2+4k+1,∴n=2k(2k+1).(k=1,2,…)①

综合上述讨论，如果令n=2k(2k+1).(k=1,2,…)由关系式（n+1）^2-n^2=(2k+1)^2 ②就可以得到无穷多个勾股数组，而且由于n和n+1是相邻整数，它们必无公因数，因而这样得到的勾股数组都是基本勾股数组。例如，分别取k=1,2,3,4,5,由①及②式得到

也就是说，得到了基本勾股数组（3,4,5）,（5,12,13），（7,24,25），（9,40,41），（11,60,61）.

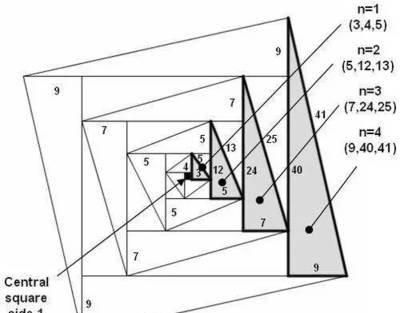
勾股弦图变式

若需要，我们还可以继续算下去，可求得无穷多组基本勾股数组。不过问题并没有完全解决，因为还不能断定这样做下去能否把所有的基本勾股数组都找出来。

至此，聪明的朋友大概已经想到，代替前面的数列II，构造一个新的数列III：

它由数列I的相隔一数的两数差构成，不难得到，III的通项公式为

（n+2）^2-n^2=4(n+1)=2^2(n+1).(n=1,2,…)

它是由除4以外的所有4的倍数构成。因而数列III中包含了除了2以外的所有偶数的平方数：4^2,6^2,8^2，…它们分别来自25与9,100与64,289与255，…之差。也就是说，得到了勾股数组（3,4,5）；（6,8,10）；8,15,17；…（3,4,5）由前面已经得到，（6,8,10）不是基本勾股数组；（8,15,17）是基本勾股数组，这样我们又得到了一组新的基本勾股数组。当然，由此还可以得到其他的新的基本勾股数组。例如取12^2，由4(n+1)=144，得n=35,即有37^2-35^2=12^2.得到了基本勾股数组（12,35,37）.同理，我们还可以构造更多的数列，他们分别由数列I的每隔二数、三数、…的两数之差构成。然后再去找其中的平方数，讨论如前。

显然，从原则上讲，用这种增加数列的方法，可以把所以的勾股数组找出来。但遗憾的是，这个办法需要施行无限多步，而且越往后计算越繁。那么是否能得到一个计算所有勾股数组的公式呢？

前面已经讲过，求所有的勾股数组的问题，从代数上讲，是求出三元二次不定方程

a^2+b^2=c^2的全部正整数解。

不定方程的解决问题比较复杂，我们准备站在古人的肩膀上来解决这个问题。

欧洲的圣人--毕达哥拉斯

古希腊著名哲学家、数学家毕达哥拉斯(Pythagoras)的表达式为：

a=2n+1, b=2n^2+2n, c=2n^2+2n+1,其中n为正整数。

古希腊著名哲学家柏拉图（Plato,公元前427～公元前347）的表达式为：

A=2n, b=n^2-1, c=n^2+1,其中n为大于1的正整数。

这两个公式都不可以求出所有的勾股数组，甚至连基本勾股数组也求不全（请自行举例）。

丢番图的墓志铭

公元3世纪，古希腊数学家丢番图（Diophantus，约246~330，代数学鼻祖）才获得较为完善的勾股数组的表达式：a=2mn,b=m^2-n^2, c=m^2+n^2,其中m>n，m,n为正整数。这是大家熟悉且常用的表达式。利用上述结果仍然不能算出所有的勾股数组（很多教师，书籍上都认为它可以找到所以的勾股数组，这是错的），例如（9，12，15）这组数就不包含在上面的结构中（不管m，n取什么正整数，这组数是不能得出来的，请您自己算一下）。尽管如此，人们还是对丢番图的结果感兴趣。因为，在上述结论的基础上，只要将勾股数组乘以正整数就可以获得一切了。

也就是说这个公式可以得到所有的基本勾股数组。

证明：

当m,n有相同的奇、偶性时，c是偶数，（a,b,c）不是基本勾股数组，因而只有当a,b为一奇一偶时，（a,b,c）才可能是基本勾股数组。事实上，这时由

（2mn）^2+（m^2-n^2）^2=（m^2+n^2）^2.

（a,b,c）为一组勾股数组。又由c+b=2m^2,c-b=2n^2。所以c,b的任何公因数，必是2m^2和2n^2的公约数，而因m,n互质，所以m^2,n^2互质，即2m^2和2n^2的公约数是2和1.所以，c,b的公约数也只能是2和1.又因为m,n一奇一偶，b,c都是奇数，因而b,c互质。所以（a,b,c）是基本勾股数组。

综上所述，我们得到著名的基本勾股数组公式：

a=2mn,b=m^2-n^2, c=m^2+n^2,其中m>n，m,n为两个互质的正整数，且为一奇一偶。

把上述得到的各数分别乘以k倍即可得到所有的勾股数组形式：

a=2kmn,b=k(m^2-n^2), c=k(m^2+n^2)。

欧几里得

出人意料的是，在丢番图出生前大约600年左右，几何学鼻祖欧几里得（Euclid，约公元前300年）已发现了勾股数组的另一表达式：

a=(p-q)/2, b=√(pq), c=(p+q)/2 其中p，q奇偶性相同，p>q，p，q是完全平方数。

而且值得肯定的是，欧氏结果虽然没有用正整数来表示也并不比丢氏的结果逊色。因为，只要令p=2m^2,q=2n^2就可以得到丢氏的那个结论。如果令p=27,q=3, 就可以得到丢氏中没有得到的勾股数组（9，12，15）。可惜的是，它的可操作性实在太差。

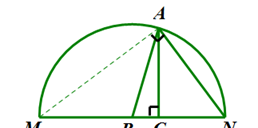
很有可能，几何学鼻祖欧几里得是用几何方法获得上述表达式的：如图，以直角三角形ABC的斜边AB为半径，以B点为圆心作半圆（MN为直径）。设AB =c（整数），AC=b（整数），CB=a（整数），则MC=MB+BC=c+a=p（整数），CN=BN-BC=c-a=q（整数）。

解得a=(p-q)/2, c=(p+q)/2，而AC=√(MC﹒CN),故b=√pq，即是上面欧氏的结果。

温馨提示：通过以上关于一位高中数学教师眼中的“勾股定理”（续二） 勾股数组内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。