北师大版初一三角形题目(北师大版七年级下册数学三角形知识点)
北师大版初一数学,三角形知识点和复习题
【知识要点】
中垂线的定义与性质(1)定义:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线(中垂线)垂直平分线,简称“中垂线”.
(2)性质:
①垂直平分线垂直且平分其所在线段.
②垂直平分线上任意一点,到线段两端点的距离相等.
③三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相等.
角平分线的定义与性质(1)定义:从一个角的顶点引出一条射线,把这个角分成两个完全相同的角,这条射线叫做这个角的角平分线
(2)性质:角的平分线上的点到角的两边的距离相等.
注意:
①这里的距离是指点到角的两边垂线段的长;
②该性质可以独立作为证明两条线段相等的依据,有时不必证明全等;
③使用该结论的前提条件是图中有角平分线,有垂直角平分线的性质语言:
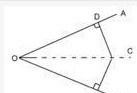
如图,∵C在∠AOB的平分线上,CD⊥OA,CE⊥OB∴CD=CE
 三角形的三线:高线、角平分线、中线
三角形的三线:高线、角平分线、中线(1)从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高.
(2)三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
(3)三角形一边的中点与此边所对顶点的连线叫做三角形的中线.
三角形的三心:内心:三条角平分线的交点
垂心:三条高线的交点
重心:三条中线的交点
【特殊三角形的性质】等腰三角形(1)等腰三角形的概念
有两条边相等的三角形叫做等腰三角形.
(2)等腰三角形的性质
①等腰三角形的两腰相等
②等腰三角形的两个底角相等.【简称:等边对等角】
③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.【三线合一】
(3)在①等腰;②底边上的高;③底边上的中线;④顶角平分线.以上四个元素中,从中任意取出两个元素当成条件,就可以得到另外两个元素为结论.
等边三角形(1)等边三角形的定义:三条边都相等的三角形叫做等边三角形,等边三角形是特殊的等腰三角形.
①它可以作为判定一个三角形是否为等边三角形的方法;
②可以得到它与等腰三角形的关系:等边三角形是等腰三角形的特殊情况.在等边三角形中,腰和底、顶角和底角是相对而言的.
(2)等边三角形的性质:等边三角形的三个内角都相等,且都等于60°.
等边三角形是轴对称图形,它有三条对称轴;它的任意一角的平分线都垂直平分对边,三边的垂直平分线是对称轴.
直角三角形两个一半定理:
(1)30度角所对的直角边等于斜边的一半。
(2)直角三角形斜边的中线等于斜边的一半。
等腰直角三角形(1)两条直角边相等的直角三角形叫做等腰直角三角形.
(2)等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.即:两个锐角都是45°,斜边上中线、角平分线、斜边上的高,三线合一,等腰直角三角形斜边上的高为外接圆的半径R,而高又为内切圆的直径(因为等腰直角三角形的两个小角均为45°,高又垂直于斜边,所以两个小三角形均为等腰直角三角形,则两腰相等);
黄金三角形黄金三角形:黄金三角形是一个等腰三角形,其腰与底的长度比为黄金比值.
黄金三角形分两种:①等腰三角形,两个底角为72°,顶角为36°;②等腰三角形,两个底角为36°,顶角为108°
【练习】
1.如图所示,在△ABC中,AB=AC,AD⊥BC于D,△ABC的周长为36,AD=12,则△ADC的周长为 .
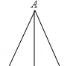
2.如图,△ABC中,AB=AC,∠BAC=40°,AD是中线,BE是高,AD与BE交于点F,则∠AFE= .
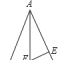
3.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若CD=BD,点D到边AB的距离为6,则BC的长是( )
A.6 B.12 C.18 D.24
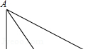
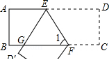
4.如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为 .
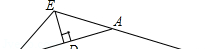
5.如图,△ABC中,AB=AC,AB的垂直平分线交AB于点D,交CA的延长线于点E,∠EBC=42°,则∠BAC=( )
A.159° B.154° C.152° D.138°
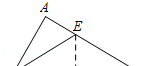
6.如图,Rt△ABC中,∠A=90°,∠ABC=56°,将△ABC沿着DE翻折,使得点C恰好与点B重合,连接BE,则∠AEB的度数为( )
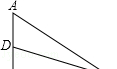
7.如图,在Rt△ABC中,∠B=90°,CD是∠ACD的平分线,若BD=2,AC=8,则△ACD的面积为 .
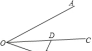
8.如图,OC平分∠AOB,D为OC上一点,DE⊥OB于E,若DE=5,则D到OA的距离为 .
温馨提示:通过以上关于北师大版初一数学,三角形知识点和复习题内容介绍后,相信大家有新的了解,更希望可以对你有所帮助。