直线射线线段教学设计(直线,射线,线段有什么联系和区别)

直线，射线，线段

提要

直线，射线，线段是最简单的几何图形，以后学习的三角形，四边形等都是由它们构成的，所以，直线，射线，线段是今后研究比较复杂图形的必要基础。要注意几何图形的表示方法，几何语言的表达，几何图形的画法，是系统学习几何知识所必需的基础，要注意线段的计数方法是其他计数问题的基本方法。

知识点

一．线段

（1）特征：①线段是直的；②线段有两个端点。

（2）表示方法：用表示它端点的两个大写英文字母来表示，也可用一个小写字母来表示。如图1-1所示的线段可以这样来表示：线段AB或线段BA或线段a。

（1）性质：两点之间的所有连线中，线段最短，简称两点之间线段最短。

一．射线

（1）特征：①只有一个端点；②向一方无限延伸。

（2）表示方法：用两个大写字母来表示，端点字母必须写在前面，另一个字母是射线上的任一点。如图1-2所示的射线可以这样来表示：射线OA或OB。

提示：两条射线为同一射线必须同时具备：①端点是同一点；②延伸方向相同，这两个条件缺一不可。

二．直线

（1）特征：①没有端点；②向两方无限延伸。

（2）表示方法：在直线上任取两点，用表示这两点的大写字母来表示，也可以用一个小写字母来表示。如图1-3所示的直线可以表示为直线AB或直线BA或直线a。

（3）性质：两点确定一条直线。

三．两点的距离

两点之间的线段的长度称为这两点之间的距离。

方法点拨

类型1 线段的计算

例1 已知线段AB=8cm，直线AB上有一点C，且BC=2cm，M是线段AC的中点，求线段AM的长。

【分析】因为点C 是直线AB上的一点，所有点C可能在线段AB上，也有可能在线段AB的延长线上，故需要分情况讨论。

【解答】（1）当点C在线段AB上时（图1-4），AC=AB-CB=8-2=6cm，AM=1/2AC=1/2×6=3cm

（2）当点C在线段AB的延长线上时（图1-5），AC=AB+BC=8+2=10cm，AM=1/2AC=1/2×10=5cm

∴AM的长为3cm或5cm。

【点评】题目中没有明确点的位置时，应该全面考虑，注意条件下的图形的多样性，防止漏解。

类型2 直线的计数

例2 观察图1-6中的①，有点A和点B可确定___条直线；观察图1-6中的②，由不在同一直线上的三点A,B和C最多能确定___条直线。

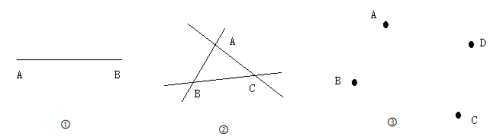
（1）动手画一画图1-6中的③中经过A,B,C,D四点的所有直线，最多共可确定___条直线。

（2）同一平面内任三点不在同一直线的五个点最多能确定___条直线，n个点(n≥2)最多能确定___条直线。

【分析】根据两点确定一条直线可得出图1-6中①的答案；动手画出图形可得出图1-6中②的答案，注意根据特殊性总结出一半规律。

【解答】图1-6①由点A和点B可确定1条直线；

图1-6②由不在同一直线上的三点A,B和C最多确定3条直线；

经过A,B,C,D四点最多能确定6条直线。

在同一平面内任三点不在同一直线的五点做多能确定10条直线。

根据一个点，两个点，三个点，四个点，五个点的情况可总结出n个点(n≥2)时最多能确定n(n-1)/2条直线。

【点评】处理这类规律探究题的基本思路是由特殊到一般，先通过特殊 情形的探究，总结规律，进而得到一般性的结论。

温馨提示：通过以上关于直线，射线，线段内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。