并查集 数据结构(查询数据结构)

数据结构—并查集《下》

 数据结构—并查集《上》主要介绍了 Quick Find 的思想和代码实现，本节要介绍的是 Quick Union的实现和代码实现。

Quick Union - UnionQuick Union的union(v1, v2)：让 v1 的根节点指向 v2 的根节点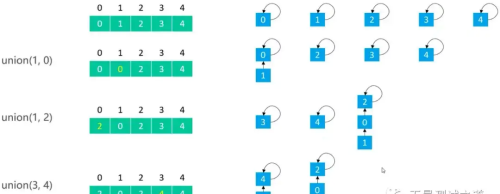

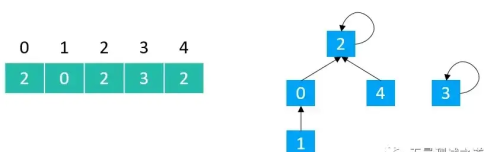
public void union(int v1, int v2) {    int p1 = find(v1);    int p2 = find(v2);    if (p1 == p2) return;    parents[p1] = p2;}

时间复杂度：O(logn)

public int find(int v) {    rangeCheck(v);    while (v != parents[v]) {        v = parents[v];    }    return v;}find(0) == 2find(1) == 2find(2) == 2find(3) == 3find(4) == 2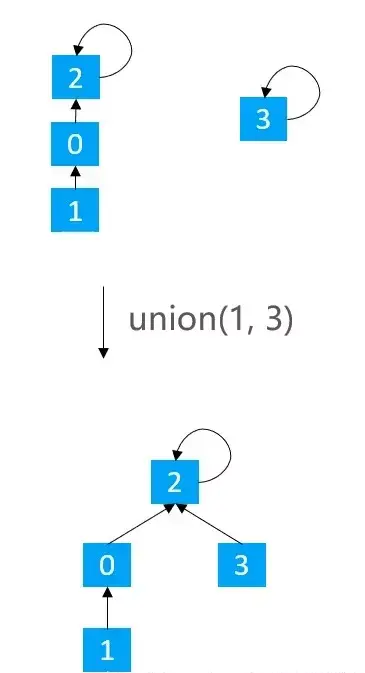

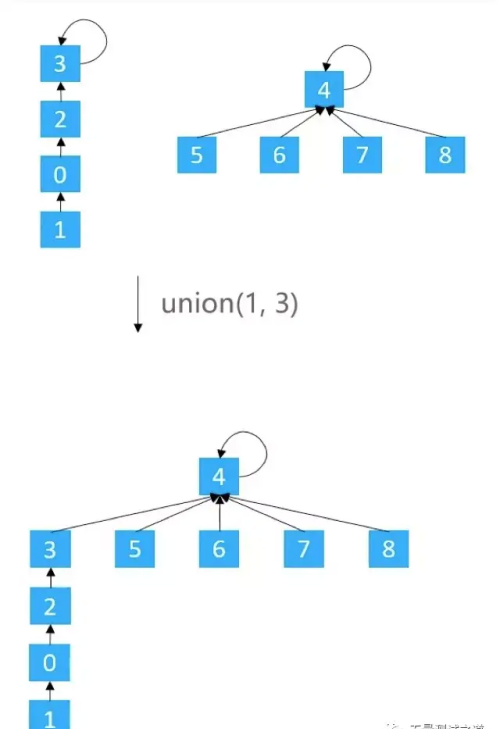
Quick Union - 优化在 Union 的过程中，可能会出现树不平衡的情况，甚至退化成链表

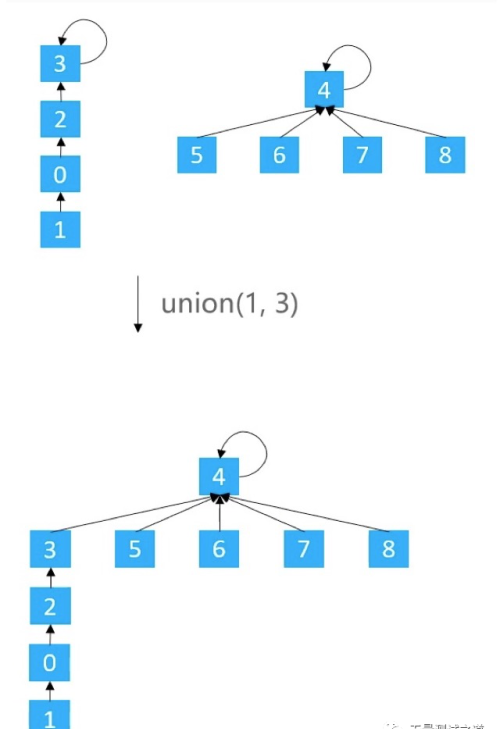
有2种常见的优化方案基于size的优化：元素少的树嫁接到元素多的树基于rank的优化：矮的树嫁接到高的树Quick Union - 1.基于 size 的优化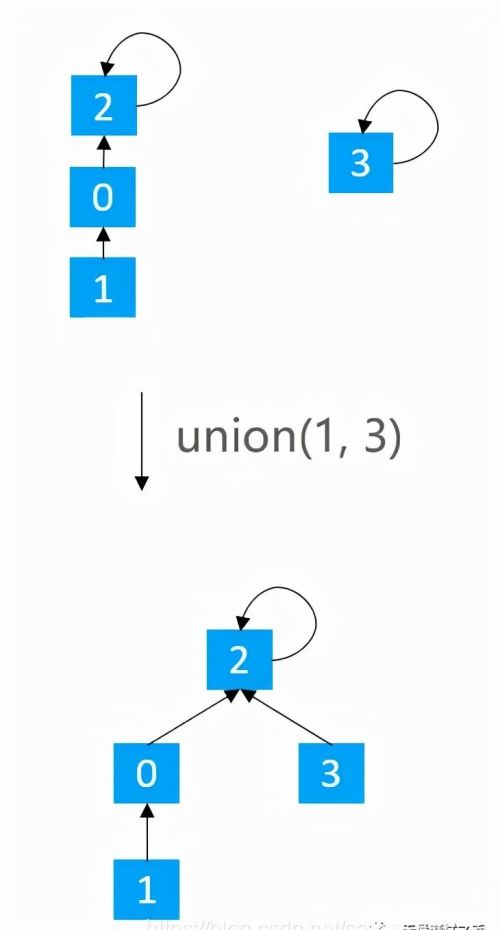

sizes = new int[capacity];for (int i = 0; i < sizes.length; i++) {    size[i] = 1;}private int[] sizes;public void union(int v1, int v2) {    int p1 = find(v1);    int p2 = find(v2);    if (p1 == p2) return;    if (sizes[p1] < sizes[p2]) {        parents[p1] = p2;        sizes[p2] += sizes[p1];    } else {       parents[p2] = p1;       sizes[p1] += sizs[p2];            }}

基于 size 的优化，也可能会存在树不平衡的问题

Quick Union - 2.基于 rank 的优化

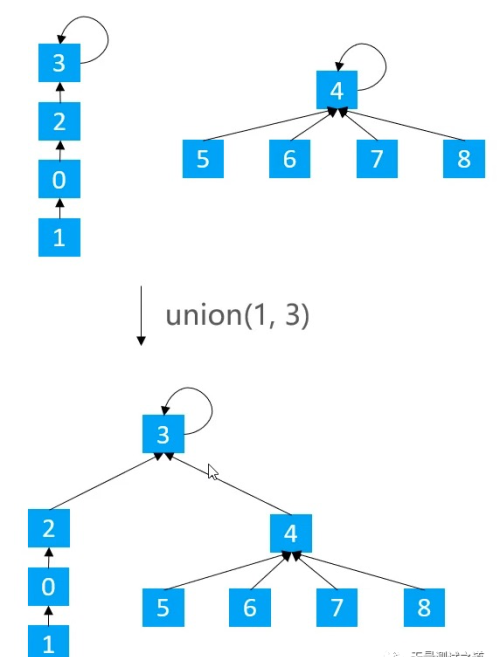
ranks = new int[capacity];for (int i = 0; i < ranks.length; i++) {    ranks[i] = 1;}private int[] ranks;public void union(int v1, int v2) {    int p1 = find(v1);    int p2 = find(v2);    if (p1 == p2) return;    if (ranks[p1] < ranks[p2]) {        parents[p1] = p2;    } else if (ranks[p2] < ranks[p1]) {        parents[p2] = p1;    } else {       parents[p1] = p2;       ranks[p2]++;    }}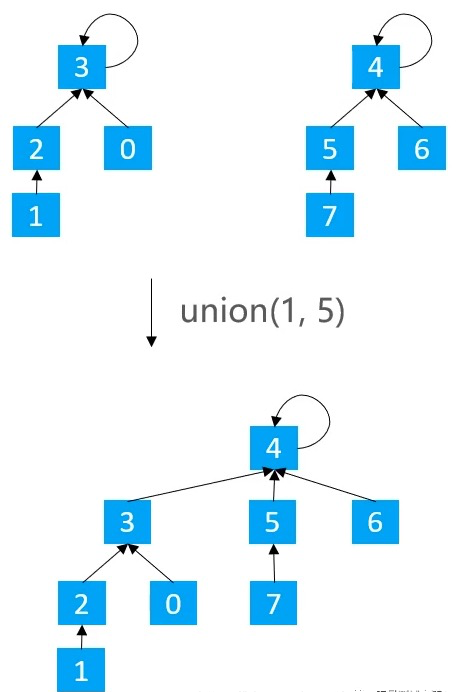

压缩路径（Path Compression）虽然有了基于 rank 的优化，树会相对平衡一点但是随着 Union 次数的增多，树的高度依然会越来越高，导致find操作变慢，尤其是底层节点（因为 find 是不断向上找到根节点）什么是路径压缩？在 find 时使路径上的所有节点都指向根节点，从而降低树的高度

public int find(int v) {rangeCheck(v);if (parents[v] != v) {    parents[v] = find(parents[v]);}return parents[v];}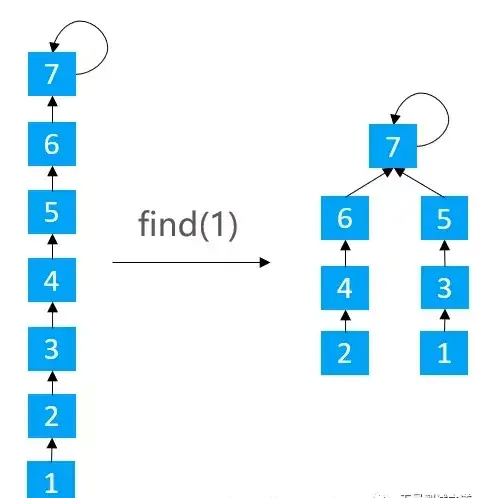

路径压缩使路径上的所有节点都指向根节点，所以实现成本稍高还有2种更有效的做法，但不能降低树高，实现成本也比路径压缩低路径分裂（Path Spliting）路径减半（Path Halving）路径分裂、路径减半的效率差不多，但是都比路径压缩要好1.路径分裂（Path Spliting）路径分裂：使路径上的每个节点都指向其祖父节点（parent的parent）

public int find(int v) {    rangeCheck(v);    while (v != parents[v]) {        int parent = parents[v];        parents[v] = parents[parent];        v = parent;    }    return v;}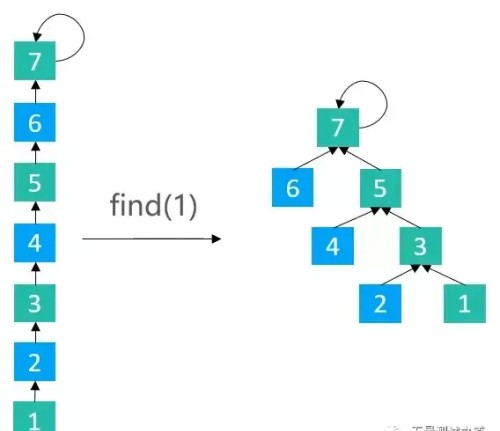

2.路径减半（Path Halving）路径减半：是路径上每隔一个节点就指向其祖父节点（parent的parent）

public int find(int v) {    rangeCheck(v);    while (v != parents[v]) {        parents[v] = parents[parents[v]];        v = parents[v];    }    return v;}

总结

  今天主要讲解了 Quick Union 的原理和代码实现。然后讲解了基于 size 和基于 rank 的优化。最后简单的介绍了下路径压缩。并查集到这就讲完了，希望给大家的知识库增加一些新的知识储备。

温馨提示：通过以上关于数据结构—并查集《下》内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。