cos(α–β)证明(证明cos(π/2-a)=sia)

多种方法证明cos45°+cos 75°=cos15°

多种方法证明cos45°+cos75°=cos15°

证法1：

利用三角的和差化积公式

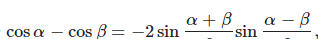
我们得到：

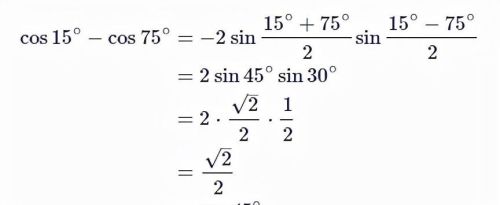
所以有：cos45°+cos75°=cos15°

证法2：如图直角三角形，斜边为1, CD=y, DB=x

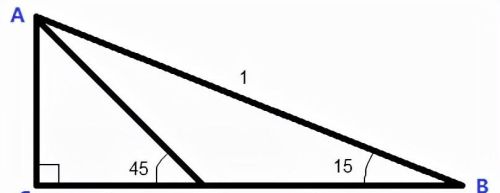
显然有cos75°=y,

在三角形ADB中利用正弦定理1/sin135°=x/sin30°,

所以x=√2/2=cos45°

x+y=cos75°+cos45°

而cos15°=x+y

因而cos45°+cos75°=cos15°

证法3：如图半圆的直径为1，

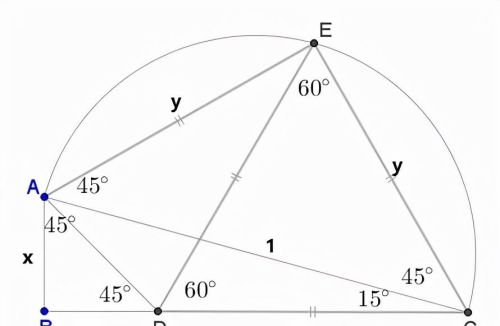
那么在三角形AEC中有cos45°=y,

在三角形ABC中有cos75°=x,

因此： cos45°+cos75°=y+x,

而在三角形ABC中有cos15°=x+y

所以cos45°+cos75°=cos15°

温馨提示：通过以上关于多种方法证明cos45°+cos 75°=cos15°内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。