baggig与随机森林(随机森林与gbdt)

集成学习：Bagging和随机森林

集成学习

俗话说：“三个臭皮匠，赛过诸葛亮”，这个道理同样适用于机器学习中。前文介绍了包括决策树在内的分类算法，都是单个的分类器，那么如果将多个分类器联合在一起应用，理论上是可以取得更好的效果，这就是集成学习的基本思想。

集成学习，或者说集成算法，就是将多个学习器集合起来，用来提高分类和预测的准确度。具体的实现方式即是从原数据抽取n个数据集训练n个弱分类器（臭皮匠），再把多个弱学习器组合后就可以成为强学习器（诸葛亮）。

弱分类器可以是同一类型的分类器，比如都是决策树；也可以是不同类型的，把分类树、逻辑回归、KNN等都用上。

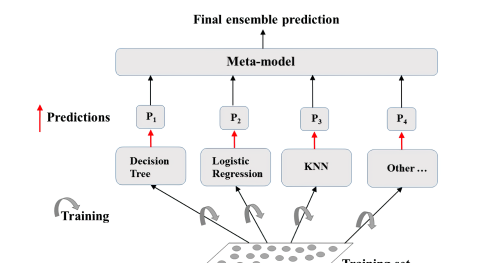
集成学习示意图

最简单的组合方法就是投票分类器（voting classifier），多个弱分类器的结果进行投票来决定最终的结果。

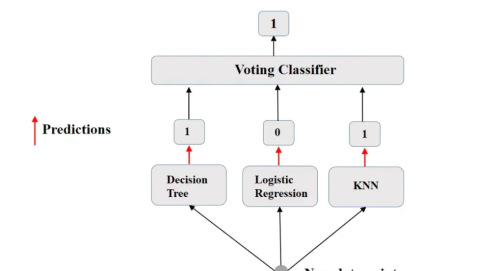
voting classifier

集成学习的框架

集成学习的弱分类器首先应该是有差异的，如果都是一样的，就起不到相互补充和加强的作用了。如何选择数据样本来训练出有差异的弱分类器，并将这些弱分类器的结果结合起来，这就需要一定的集成学习框架来组织。

总的来说集成学习主要有三种框架：

Bagging（装袋）Boosting（提升）Stacking（堆叠）

Bagging

Bagging装袋又称自主聚集(bootstrap aggregating)，是一种根据均匀概率分布从数据集中重复抽样的技术。重复抽样，又称为有放回的抽样，每次被抽中的单位都再被放回总体中参与下一次抽样。每个新数据集和原始数据集大小相等。

Bagging的主要特征就是并行训练一堆分类器，代表算法为随机森林 （random forest）。由于每一个分类器，也就是每一棵树都不一样，因此减少了分类器的随机性，也就是保证了整个预测结果的稳定性。

Boosting

Boosting提升策略是一个迭代的过程，用来自适应地改变训练样本的分布，使得弱学习器聚焦到那些很难分类的样本上。弱学习器的结果也将被赋予不同的权重。

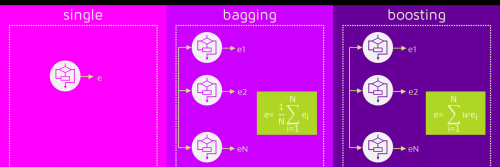
Boosting算法中不同分类器结果有不同的权重

Bagging框架对各个分类器的训练是并行的，而Boosting框架对分类器的训练是串行的。关于Boosting框架将在后面的文章中进行更多地介绍。

Stacking

Stacking是一种分层模型集成框架。以两层为例，第一层由多个基学习器组成，其输入为原始训练集，第二层的模型则是以第一层基学习器的输出作为特征加入训练集进行再训练，从而得到完整的Stacking模型。

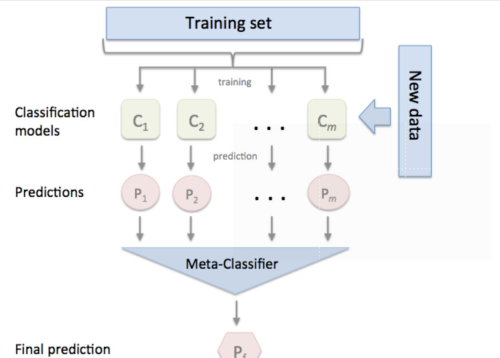
Stacking：第一层分类器输出为第二层分类器的输入

Bagging

本文重点介绍一下Baggnig集成学习的实现方式，对于其他的集成学习算法，在之后的文章中再进行介绍。

Bagging的实现方式

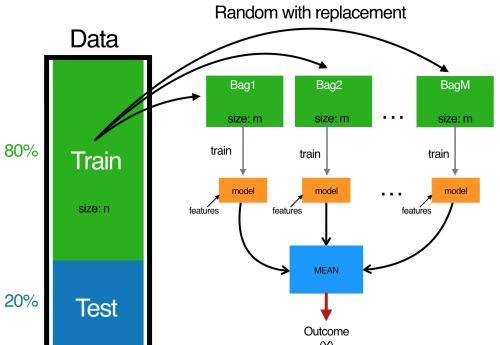
Bagging的过程

假设有一个数据集，通过Boostrap(自助抽样)有放回的抽样n次，那么产生了n个样本数据集，记为n个train数据集。将这n个train集进行训练，因此产生了n个基分类器（ID3、C4.5、CART等），即n个决策树。利用这n个基分类器对测试集进行预测，因此会得到n个结果。基于n个基分类器的结果，计算平均值得到最终预测；或者采取多数投票（majorty vote），即将n个预测的结果出现频率最高的类作为总体预测。

Bagging的不足

如果一个数据集有一个很强的预测变量和一些中等强度的预测变量，那么大多数的树都会将最强的预测变量用于顶部分裂点，这会造成所有的树看起来都很相似。在这种情况下，装袋法与单棵树相比不会明显降低方差。为了解决这个问题，随机森林在Bagging基础上又进行了改进。

随机森林

随机森林是用随机的方式建立一片森林，森林由决策树组成，每一棵决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本需要分类，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类，然后看看哪一类被选择最多，就预测这个样本为哪一类。

那么随机森林算法如何保证决策树之间没有关联呢？关键就在于弱分类器构造的两个关键点：

数据采样随机特征选择随机

具体地说，随机森林在Bagging基础上做了以下改进：

依旧是样本集中用Bootstrap采样选出n个样本从所有属性中随机选择k个属性，选择最佳分割属性作为节点建立CART决策树。重复以上两步m次，即建立了m棵CART决策树这m个CART形成随机森林，通过投票表决结果，决定数据属于哪一类。

由于随机森林中的子树的每一个分裂过程并未用到所有的待选特征，而是从所有的待选特征中随机选取一部分特征，之后再在随机选取的特征中选取最优的特征。这样能够使得随机森林中的决策树都能够彼此不同，提升系统的多样性，从而提升分类性能。

主要影响随机森林性能的因素有两方面：

森林中单棵树的强度（strength）：每棵树的强度越大，则随机森林的性能越好森林中树之间的相关度（correlation）：树之间的相关度越大，则随机森林的性能越差

关于Bagging和随机森林，本文先讲这么多，后续再讲一些前文提到的Boosting的集成算法。

温馨提示：通过以上关于集成学习：Bagging和随机森林内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。