立体几何垂直证明技巧(立体几何垂直怎么证)
立体几何垂直证明的六大绝招,一看就会
六大绝招
类型一
利用已知垂直关系证垂直
例题:已知△ABC中,∠ACB=90°,SA⊥面ABC,AD⊥SC,求证:AD⊥面SBC
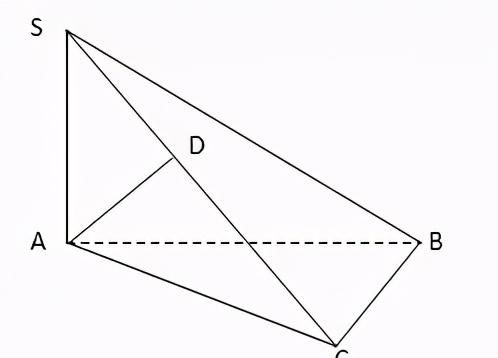
证明:
∵SA⊥面ABC ∴SA⊥BC
又∠ACB=90° ∴AC⊥BC
又AC,SA⊆面SAC ∴BC⊥面SAC
∴BC⊥AD
又AD⊥SC
且BC,SC⊆面SBC
∴AD⊥面SBC
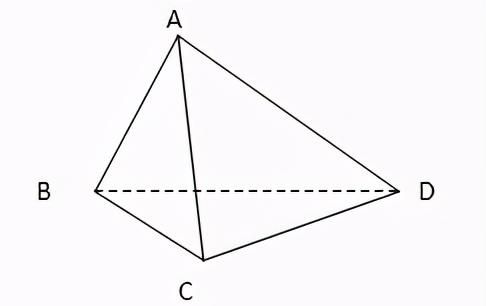
变式:如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,求证:AD⊥AC
类型二
利用等腰三角形中线证垂直
例题:在三棱锥P-ABC中,AC=BC,AP=BP,求证PC⊥AB
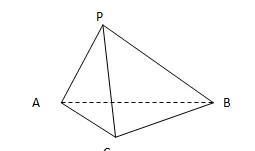
证明:
取AB的中点M,连接PM,CM
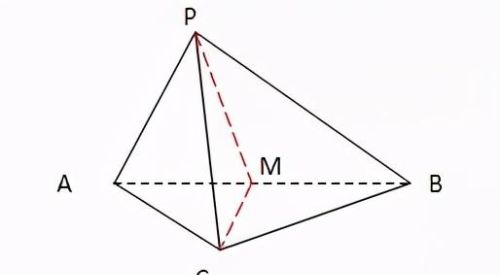
∵AC=BC,M是AB的中点,∴AB⊥CM
∵AP=BP,M是AB的中点,∴AB⊥PM
∴AB⊥面PCM
∴AB⊥PC
变式:四棱锥P-ABCD,底面ABCD是正方形,PA=AD,求证面PAD⊥面PCD
类型三
利用勾股定理逆定理证垂直
例题:如图,四棱锥P-ABCD的底面是边成为3的正方形,PA⊥CD,PA=4,PD=5,求证:PA⊥面ABCD
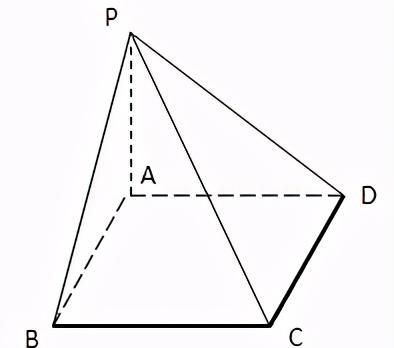
证明:
∵PA=4,AB=3,PD=5
∴PA2+AB2=PD2,
∴三角形PAD是直角三角形,
∴PA⊥AD
又PA⊥CD,
∴PA⊥面ABCD
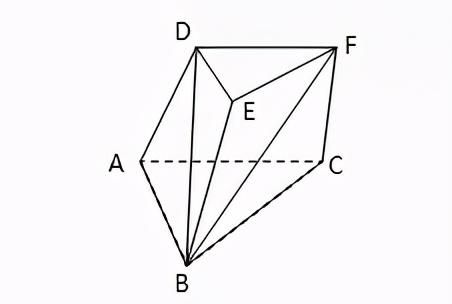
变式:如果,在三棱台ABC-DEF中,平面BDEF⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,求证:BF⊥面ACFD
类型四
利用三角形全等证垂直
例题:如图,三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°,求证:AB⊥PC
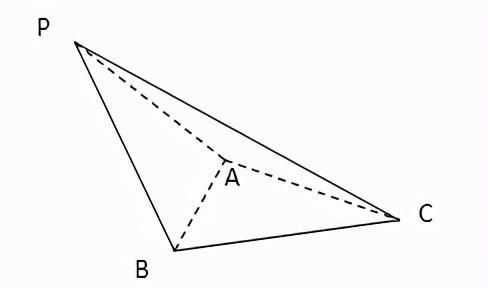
证明:
取AB的中点M,连接CM,
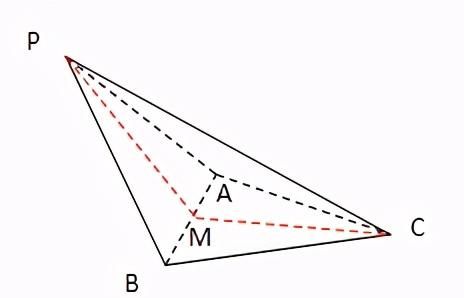
∵△PAB是等边三角形,∴PB=PA
又PC=PC,∠PAC=∠PBC=90°
∴△PBC≌△PAC,∴BC=AC
∴△ACB是等腰三角形,M是AB的中点,
∴CM⊥AB
又在等边△PAB中,M是AB的中点,∴PM⊥AB
∴AB⊥面PMC
∴AB⊥PC
变式:如图,在以A、B、C、D、E、F为顶点的五面体中,平面CDEF⊥平面ABCD,FC=FB,四边形ABCD为平行四边形,且∠BCD=45°,求证:CD⊥BF
类型五
利用平行关系证明垂直
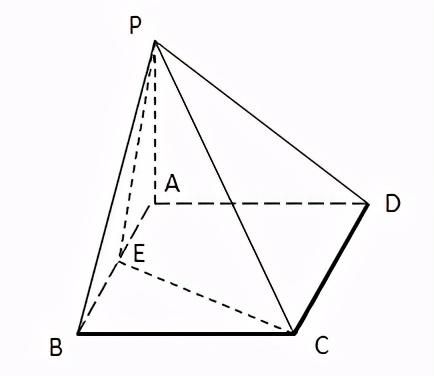
例题:如图四棱锥P-ABCD,底面是正方形,PA⊥底面ABCD,∠PDA=45°,E是棱AB的中点,求证:面PCE⊥面PCD
证明:
分别做PC,PD的中点M,N两点,连接EM,MN,NA
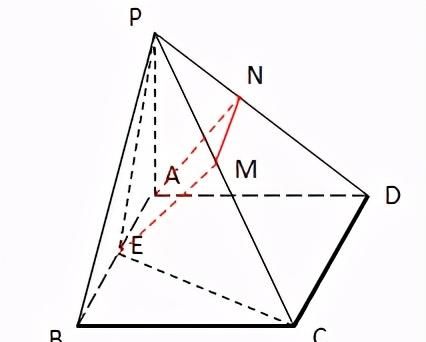
∵MN为△PCD的中位线,
∴MN∥CD且MN=1/2CD
又∵E是AB的中点,
∴AE∥CD且AE=1/2CD
∴四边形AEMN是平行四边形,则EM∥AN,
∵PA⊥面ABCD,∴PA⊥AD,
且∠PDA=45°,∴△PAD是等腰直角三角形
又N是PD中点,∴AN⊥PD
∵四边ABCD是正方形,
∴CD⊥AD,又PA⊥CD,
∴CD⊥面PAD,∴CD⊥AN,
又上面已求PD⊥AN,∴AN⊥面PCD
又∵EM∥AN,∴EM⊥面PCD
∵EM⊂面PEC,∴面PEC⊥面PCD
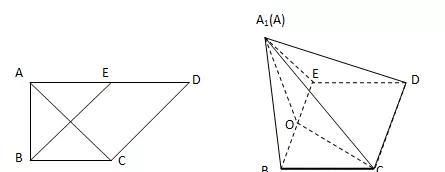
变式:如图1,在直角梯形ABCD中,AD∥BC, ∠BAD=90°,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2,证明CD⊥面A1OC.
类型六
利用向量数量积证明垂直
例题:如图所示,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD,证明:PA⊥BD。
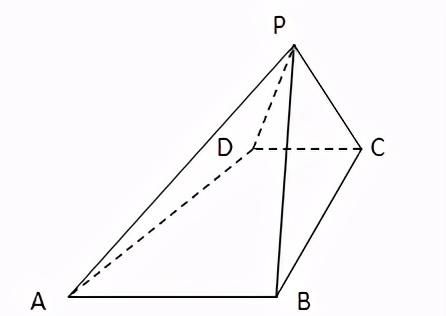
证明:
取BC得中点O,连结PO,
∵平面PBC⊥底面ABCD,△PBC为等边三角形
∴PO⊥底面ABCD
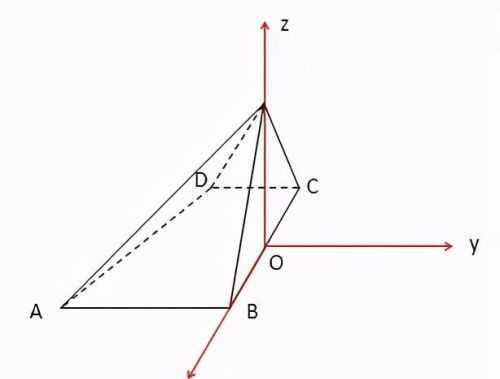
以BC的中点O为坐标原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,OP所在直线为z轴,建立空间直角坐标系如下:

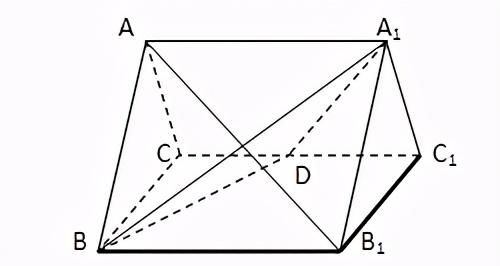
变式:如图,正三棱柱ABC-A1B1C1的所有棱长都是2,D是CC1的中点,求证:AB1⊥面A1BD
常见的平面图形垂直模型
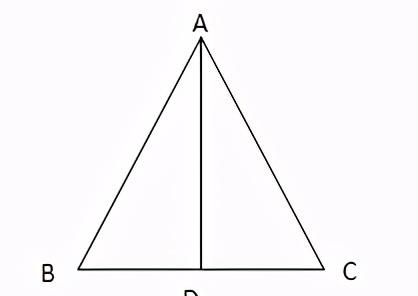
1. 等腰三角形的中线垂直底边
在△ABC中,AB=AC,D为BC的中点,则有:AD⊥BC
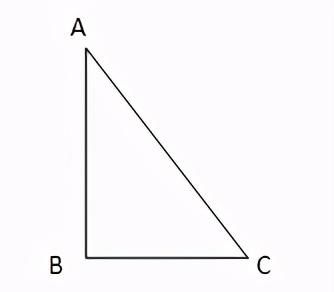
2. 勾股定理的逆定理得到垂直
在三角形中,如果AB2+BC2=AC2,则有:AB⊥BC
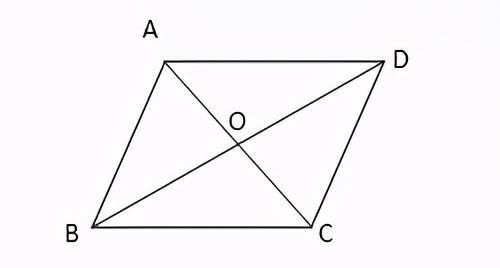
3. 菱形的对角线互相垂直
已知四边形ABCD为菱形,两条对角线AC与BD相交与点O,则有:AC⊥BD
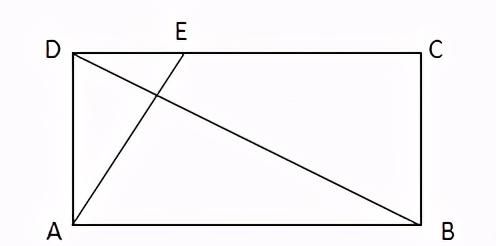
4. 矩形内部线段存在的垂直关系
四边形ABCD为矩形,如果AD:DE=AB:AD,则有:BD⊥AE
5. 直角梯形内部线段存在的垂直关系
a. 四边形ABCD为直角梯形,且CD⊥AD,CD∥AB,如果AD:DC=AB:AD,则有:BD⊥AC
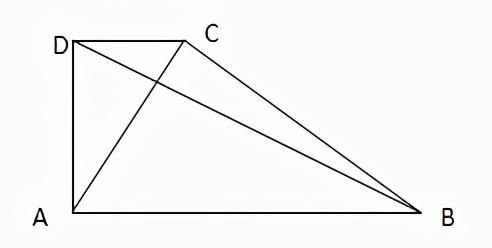
b. 四边形ABCD为直角梯形,且CD⊥AD,CD∥AB,如果AD=DC=m,AB=2m,则
有:AC⊥BC
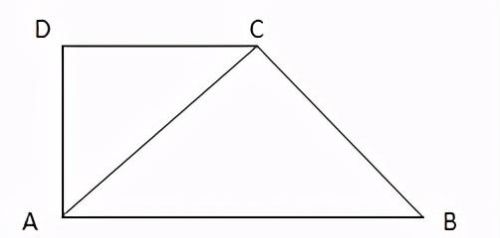
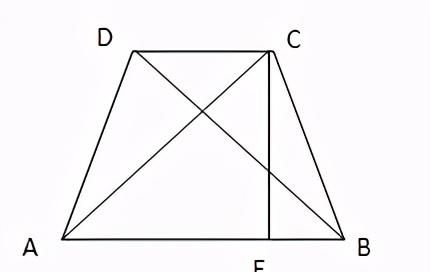
6. 等腰梯形内部线段存在的垂直关系
四边形ABCD为等腰梯形,且AB∥DC,AD=BC,CE为等腰梯形ABCD的高,若CE=1/2(AB+CD),则有:AC⊥BD
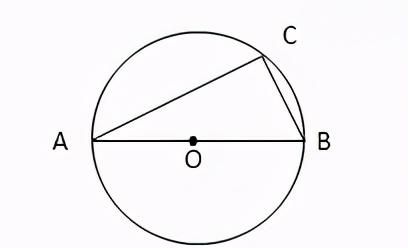
7. 圆的直径所对的圆周角为90°
AB为圆O的直径,C为圆上任意一点,则有:AC⊥BC
温馨提示:通过以上关于立体几何垂直证明的六大绝招,一看就会内容介绍后,相信大家有新的了解,更希望可以对你有所帮助。