长方形对角线所形成的角(长方形通过对角线求面积)

从长方形的对角线谈起

生活中的数学题

如果一个长方形已知长宽比和对角线长度，就可以用勾股定理和比例式计算出它的长和宽，并得到面积。

举个例子，平板电视机屏幕是15:8，对角线长度是50英寸，求电视机屏幕的长和宽各是多少？

先用勾股定理计算，如果两条直角边长度分别是15个单位和8个单位，那么斜边的长度是多少个单位？

熟悉勾股形的同学不用算，张口就报出答案:17。回答正确。列比例式计算长和宽：

50:17=x:15=y:8

解比例式，得

x=50×15÷17=44.117647

y=50×8÷17=23.529412

谈谈斜率

问题来了，电视机厂商为什么告诉你长宽比和对角线的长度，而不告诉你长和宽？

其实，厂商告诉你长宽比，就是告诉你对角线的斜率，这个参数决定了屏幕的形状。再告诉你对角线的长度，就确定了长方形的面积。

斜率是一个非常重要的数学概念。一次函数y=kx+b的图像是一条直线。b是直线在y轴上的截距，如果b=0，那么直线通过原点，截距为0。k就是斜率。

我曾经问过一位同学，正比例函数y=x的斜率是多少？这位同学居然回答不知道。看来同学没有掌握斜率的概念。

正比例函数y=x的斜率是1，它的图像可以看作正方形的对角线，通过原点，与x轴的夹角为45°。直线上任意一点的横坐标和纵坐标都相等。

y=x为什么不写成y=1x+0？因为数学的语言追求简洁而不是啰嗦。因为x=y，所以y:x=1，所以斜率k=1。

一个正比例函数的图像上有一个点的坐标是(1，2)，请写出函数的解析式。

因为是正比例函数，所以解析式为y=kx，根据题目给出的坐标，斜率k=2:1=2，所以，解析式为：y=2x

因为正比例函数的图像通过原点，两点确定一条直线，所以能够求出斜率。

对于一次函数的图像，知道了两点的坐标，就能够求出直线的斜率。

已知直线y=kx+b上任意两点的坐标，就可以用下面的公式求出斜率：

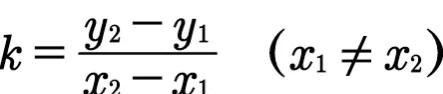
图片

举个例子。一条直线通过两点(-2，0)和(3，5)，求它的斜率。

把两点坐标代入上面的公式计算，所求斜率为1。

学习了三角函数后，我们对斜率有了更为深入的认识和理解。

直线y=kx+b和通过原点的直线y=kx平行，所以它们和x轴的正方形向形成的两个交角相等(同位角)。设直线y=kx和横轴的交角是α，那么

图片

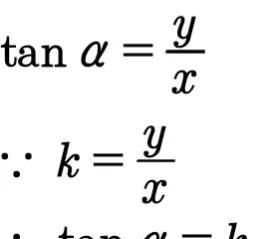
这样一来，直线的斜率就有了更明确的意义，就是：“直线和横轴的交角的正切，叫做这直线的斜率。”

微博上有个账号叫库库数学，做了一个在棋盘格上打高尔夫球的游戏。你只需要在函数解析式填入合适的斜率，球员就能够准确地一杆进洞。如果你填入错误的斜率，也能够看到高尔夫球的运行轨迹，与目标的偏差有多大，迅速得到反馈。这个有趣的游戏可以检验你对斜率的理解是否正确。

说完了长方形的对角线，再顺便提一下正方形的对角线。

正方形边长为a，对角线为f，则f=√2a(对角线长度是边长的√2倍)，面积s=a²=½f²

面积之谜

接下来我们来看一道几何计算题。有了前面的铺垫，这道题目的难度就大大降低了。

图片

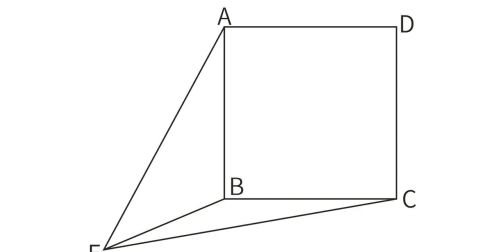
如图，四边形ABCD为正方形，E为正方形外的一点，分别连接EB、EA、EC，已知：EB=12cm，△AEB的面积为90cm²，△EBC的面积为48cm²，求正方形ABCD的面积是多少？

请大家思考一下，再揭晓答案。

解析：

EB可以看作长方形的对角线，题目告诉你两个三角形的面积，因为这两个三角形底边相等(都等于正方形的边长)，所以可以得到长方形的长宽比。前面我们已经知道，我们可以根据题目条件求出长方形的长和宽。

两个三角形的面积之比等于它们以正方形边长为底边的高之比。换句话说就是，以EB为对角线的长方形的长宽比是90:48，化简为15:8，所以长方形的长和宽分别是180/17和96/17。

因为三角形的面积，底和高这三个量可以知二求一，所以，我们可以求出正方形的边长。知道了正方形的边长a，面积s=a²，这道题就可以收工了。我们求出正方形边长为17，

所以正方形面积为

17²=(a+b)²=(a-b)²+4ab

=(10+7)²=289

你做对了吗？

科学尚未普及，媒体还需努力。感谢阅读，再见。

温馨提示：通过以上关于从长方形的对角线谈起内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。