> 房产

求正方形的周长要知道(求正方形的周长公式是什么?)

正方形-由45°确定三角形周长定值

如图，点E、F 分别是正方形ABCD边BC、CD上的点，连接AE、AF、EF，且∠EAF＝45°.

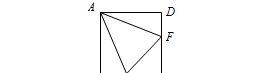
如图，将△ADF绕点A顺时针旋转90°，得到△ABG，则∠GAF＝90°.

∵∠EAF＝45°，∴∠EAG＝45°，∴∠EAF＝∠EAG.

∵AE＝AE，AG＝AD，∴△AEG≌△AEF，

∴EF＝GE＝BE＋BG＝BE＋DF.

∴△CEF的周长＝CE＋EF＋CF＝CE＋BE＋DF＋CF＝BC＋CD＝正方形边长的2倍.

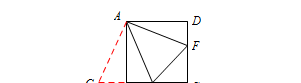
例如图，点E、F 分别是正方形ABCD边BC、CD上的点，连接AE、AF、EF，且∠EAF＝45°.

(1) 已知AB＝5，则△CEF的周长为______.

(2) 若△CEF的周长为4，则正方形的边长为______.

解析

(1) △CEF的周长＝正方形边长的2倍＝10.

(2) ∵△CEF的周长＝正方形边长的2倍，

∴正方形边长＝△CEF的周长÷2＝2.

答案 10；2

练习

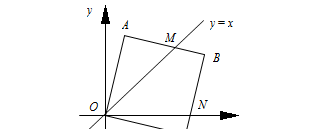
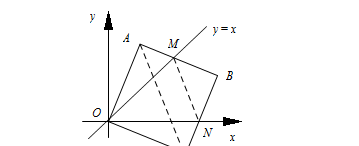
1. 在平面直角坐标系中，边长为2的正方形OABC的两个顶点A、C分别在y轴、x轴的正半轴上，点O在原点.现将正方形OABC绕点O顺时针旋转，当点A第一次落在直线y＝x上(一、三象限角平分线)时停止旋转.旋转过程中，AB边交直线于点M，BC边交x轴于点N(如图).

(1) 停止旋转时，点B的坐标为________.

(2) 旋转过程中，当MN和AC平行时，正方形OABC旋转的度数为_____.

(3) 设△MBN的周长为p.在旋转过程中，p值是否发生变化？若发生变化，说明理由.若不发生变化，请直接写出p的值：______.

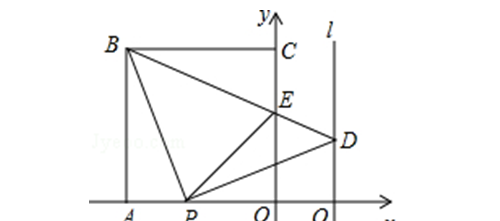
2. 如图，正方形OABC的边OA，OC在坐标轴上，点B的坐标为(﹣4，4)．点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴的正方向运动，规定点P到达点O时，点Q也停止运动．连接BP，过P点作BP的垂线，与过点Q平行于y轴的直线l相交于点D．BD与y轴交于点E，连接PE．设点P运动的时间为t(s)．

(1) ∠PBD的度数为　　，点D的坐标为　　(用t表示)；

(2) 当t为__________时，△PBE为等腰三角形.

(3) 探索△POE周长是否随时间t的变化而变化？若变化，说明理由；若不变，请直接写出周长定值：______.

解析

(1) 直线y＝x与两坐标轴夹角为45°.

A点停止旋转时，共旋转45°，则B落在x轴上.易知OB＝2，

∴B坐标为(2，0).

(2) 如图，MN∥AC，则∠BMN＝∠BNM＝∠BAC＝45°，∴BM＝BN，∴AM＝CN，易证△OMA≌△ONC，∴∠AOM＝∠CON.

∵∠AOM＋∠CON＝90°－45°＝45°，∴∠AOM＝22.5°，即旋转的度数为22.5°.

(3) ∵∠MON＝45°，∴确定：p＝2AB＝4.

答案 (1)(2，0)；(2)22.5°；(3)4

解析

(1) ∵AP＝OQ，∴AP＋OP＝OQ＋OP，即OA＝PQ.易证△ABP≌△QPD，

∴PB＝PD，AP＝DQ，∴D(t，t).∵∠BPD＝90°，∴∠PBD＝45°.

(2) ①设PB＝PE，则∠BPE＝90°．而∠BPE＜90°，∴这种情况不可能.

②设EB＝EP，则∠BEP＝90°，△POE≌△ECB．∴OE＝BC，∴点E与点C重合(EC＝0)．∴点P与点O重合(PO＝0)．∵点B(－4，4)，∴AO＝CO＝4．此时t＝AP＝AO＝4.

③设BP＝BE，∴Rt△BAP≌Rt△BCE(HL)．∴AP＝CE．∵AP＝t，∴CE＝t．∴PO＝EO＝4－t．再证EP＝CE＋AP．∴EP＝t＋t＝2t．∴(4－t)＝2t．解得：t＝4(－1).

(3) ∵∠POE＝45°，∴确定：△POE周长＝2AB＝8.

答案 (1)45°，(t，t)；(2) 4或4(﹣1)；(3)8

温馨提示：通过以上关于正方形-由45°确定三角形周长定值内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。