迪菲赫尔曼密钥交换举例(迪菲赫尔曼密码)
迪菲-赫尔曼密钥交换的实现思路和原理
迪菲-赫尔曼算法可以实现再不安全的网络实现密钥的安全交换。
假设 :A和B需要建立安全通信通道,A和B需要持有密钥解密信息,迪菲-赫尔曼算法简单说就是A和B各持有密钥P和S,并把自己持有的密钥发给对方,这样A和B都持有密钥PS,并且几乎无法通过PS得到P或者S,且密钥与顺序无关,即PS等同SP。PS可以继续合成PPS等,无限继续合成,但是无法拆解。
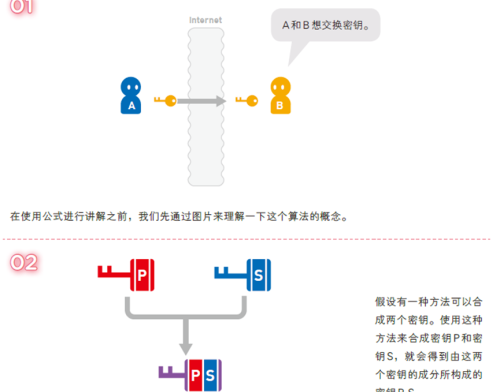
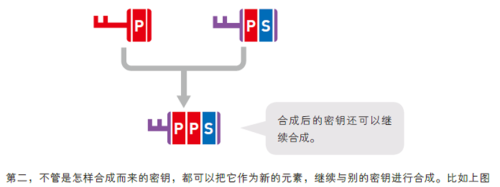
实例:
A和B欲通信,此时只有A持有密钥P,然后A将P发给B,则A和B都持有P。A和B分别准备私钥SA和SB,发给对方,则A和B分别合同PSA和PSB,然后再和自己的私钥合成SAPSB和SBPSA,由于顺序无关,此时A和B持有相同密钥,可以安全交换信息,由于即使密钥被截获也无法拆解,所以是安全的。但是,也并非完全安全,单纯的迪菲-赫尔曼算法无法规避中间人攻击。
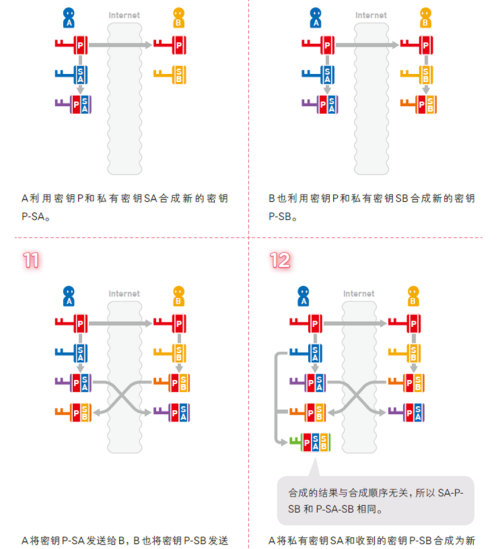
刚才是举例说明思路,下面是数学基础原理
首先,对于任一素数P,一定存在一定数量的生成元。
现在假设P是一个非常大的素数,G是P的所有生成元中的一个。A和B分别准备一个秘密数字X和Y,分别做如下计算GX mod P 和 Gy mod P,然后将结果发给对方。A和B再重复取余,由于GX y mod P 和 GyX mod P是相等的。A和B此时得到相同的结果作为密钥。

下面单独说明一下数学推导过程:
假设A,B两人通信,约定使用同一个有限循环群G和它的一个生成元g。一般过程如下:
A选择一个随机正整数a,计算ra=ga mod p发送给B。
B选择一个随机正整数b,计算rb=gb mod p发送给A。
A收到B消息后 计算R1=rba mod p
B收到A消息后 计算R2=rab mod p
由于r1==r2,所以得到同一个值,作为共同的密钥。
为什么r1==r2? 可以推导如下:
R1=rba mod p=(gb mod p)a=(gb)a mod p=gba mod pR2=rab mod p=(ga mod p)b=(ga)b mod p=gab mod p
得到R1==R2, 这里用到了指数模运算的性质。

温馨提示:通过以上关于迪菲-赫尔曼密钥交换的实现思路和原理内容介绍后,相信大家有新的了解,更希望可以对你有所帮助。