谓词逻辑:一阶语言的模型和赋值模型(谓词逻辑:一阶语言的模型和赋值方法)

谓词逻辑：一阶语言的模型和赋值

一阶语言的一个模型M（亦称“解释”）包括下列因素：

（Ⅰ）一个个体域D，即由具有一定性质的个体所构成的集合。当给定个体域之后，全称量词表示个体域中的所有个体，存在量词表示个体域中的某些个体。全称量词、存在量词和被量词约束个体变项的意义都确定了。

（Ⅱ）个体域上的解释函数I。解释函数I将一阶语言中的符号对应到它们的语义解释上。它把个体常项解释为D中的特定个体，把n元谓词符号解释为个体域上的n元关系。

当给定模型M后，谓词逻辑的闭公式的意义就确定了，其真假也确定了。

但谓词逻辑的开公式（含有自由变项的公式）的意义尚不确定，为了确定该公式的真值，需要对其中的自由变项的值做指派（记为ρ）。

一个指派是一个函数ρ：它将每个个体变项对应到个体域中的一个个体上。即对任意个体变项x，ρ(x)∈D。

在模型M和指派ρ之下，谓词逻辑的所有公式都有了确定的意义，也有了确定的真假。谓词逻辑的语言因此得到了确定的解释。

一个模型M和模型M上的一个指派ρ合称为一个赋值σ，即一个赋值σ是模型M和指派ρ的有序对，记为σ=<M，ρ>。

一个赋值又称一个解释。

公式的真值条件

形如F(t₁,…,tₙ)的公式在σ下为真，当且仅当，t₁,…,tₙ表示的那n个体域中个体确实有F表示的那个n元关系，即<σ(t₁),…,σ(tₙ)>∈σ(F)。

形如∀xA的公式在σ下为真，当且仅当，将A中自由出现的x解释为个体域中的每个个体后，A总为真。

形如∃xA的公式在σ下为真，当前仅当，将A中自由出现的x解释为个体域中的某个个体后，能使A为真。

否定式、合取式、析取式、等值式的真值条件同命题逻辑。

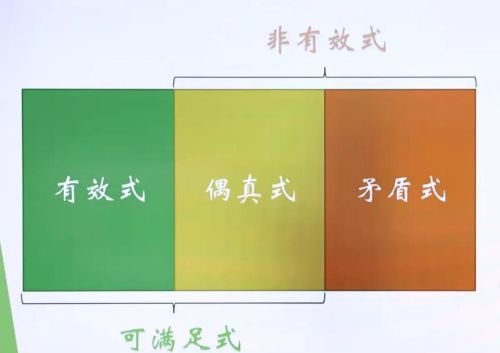
如果一个谓词逻辑的公式对于任一赋值都为真，则称该公式为普遍有效式（简称有效式，亦称常真式）。普遍有效式是谓词逻辑的规律。对比：命题逻辑中的重言式（Tautology同义反复）。

如果一个谓词逻辑的公式对于任一赋值都为假，则称该公式是一个不可满足式，亦称常假式。不可满足式是谓词逻辑中的逻辑矛盾。

如果一个谓词逻辑的公式对于有些赋值为真，对于有些赋值为假，则称该公式是偶真式，但非普遍有效式。

所有的普遍有效式和偶真式统称可满足式。

有效式举例

（1）∀xF(x)→F(y)

（2）F(y)→∃xF(x)

（3）∀x(F(x)Ⅴ¬F(x)) 排中律

（4）¬∃x(F(x)∧¬F(x))

（5）∀xF(x)↔¬∃x¬F(x)

（6）∃xF(x)↔¬∀x¬F(x)

（7）∀x(F(x)→G(x))→(∀xF(x)→∀xG(x))

（8）∀x(F(x)∧G(x))↔(∀xF(x)∧∀xG(x))

（9）∃x(F(x)ⅤG(x))↔(∃xF(x)Ⅴ∃xG(x))

（10）∃x∀yR(x，y)→∀y∃xR(x，y)前面蕴涵后面，但逆推不成立

温馨提示：通过以上关于谓词逻辑：一阶语言的模型和赋值内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。