感生电动势和动生电动势可以叠加吗(感生电动势和动生电动势的关系)

感生电动势和动生电动势共存现象

1.磁场发生变化，产生的感应电动势叫做感生电动势.

2.磁场处于稳定状态，回路中导体棒切割磁感线，产生的感应电动势叫做动生电动势.

3.常用方法：

①普适公式E=N△Ф/△t；

②感生和动生的代数和；

③利用数学求导的方法；

④利用数学求极限的方法.

例题：如图，固定于水平面上的金属架CDEF 处在竖直向下的匀强磁场中，金属棒MN 沿框架以速度 v 向右做匀速运动。t ＝ 0 时，磁感应强度为 B₀，此时 MN 到达的位置恰好使MDEN 构成一个边长为 l 的正方形。为使 MN棒中不产生感应电流，从 t ＝ 0 开始，磁感应强度 B 应该怎样随时间 t 变化？请推导出 B 与 t的关系式。

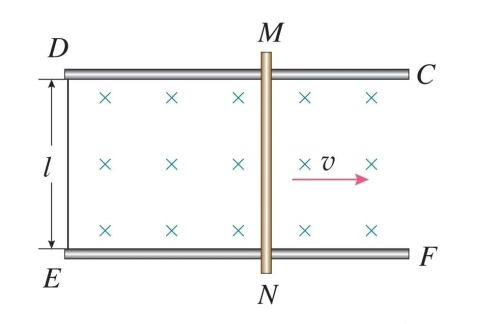
解法一：

E=0，△Ф/△t=0，△Ф=0

Ф₀=B₀S₀，Ф=BS=B(S₀+vlt)

Ф₀=B₀S₀=Ф=BS=B(S₀+vlt)

解法二：

例题：如图所示，一金属导线单位长度的电阻为ρ，折成等腰直角三角形，直角边长为a，在t＝0时刻从图示位置开始以匀速v进入以B＝B₀-kt规律变化的均匀磁场中，其中k为大于零的常数。当三角形的水平直角边进入一半时，求：

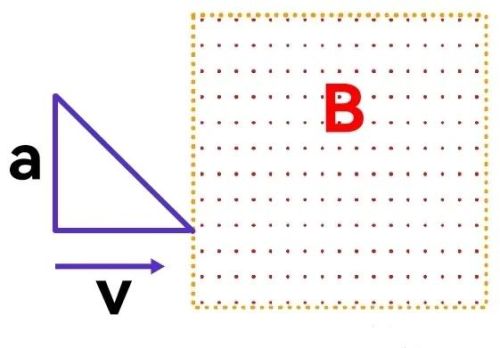
(1)导线内的动生电动势；

(2)导线内的感生电动势；

(3)导线内的感应电动势；

(4)导线内的电流强度；

(5)通过回路总电量.

【解析】

(1)当三角形的水平直角边进入一半时，经历时间为a/v.此时磁感应强度B=B₀-ka/v，切割磁感线的有效长度为a/2.

E₁=BLv=(B₀-ka/2v)av/2.

(2)当三角形的水平直角边进入一半时，经历时间为a/v.此时磁感应强度B=B₀-ka/v，磁感应强度变化率即B对t的导数为-k，回路扫过的有效面积为a²/8.

E₂=-ka²/8.(负号为电动势方向)

(3)

方法一：感应电动势等于感生电动势与动生电动势的代数和.

此时感生电动势方向和动生电动势方向相反.

E=|E₁+E₂|=|B₀av/2-3ka²/8|.

方法二：磁通量Ф对时间t求导

Ф=BS=(B₀-kt)v²t²/2

Ф′(t)=B₀av/2-3ka²/8

方法三：求△Ф/△t(△t→0)的极限

(4)感应电流等于感应电动势除以回路总电阻.

(5)通过回路总电量

q=N△Ф/R(R为回路总电阻)

例题：如图所示，两根完全相同的光滑金属导轨OP、OQ固定在水平桌面上，导轨间的夹角θ＝74°，导轨所在空间有垂直于桌面向下的匀强磁场，且磁感应强度B随时间t的变化关系为B=k/t，其中比例系数k＝2T·s。将电阻不计的金属杆放置在水平桌面上，在外力作用下，t＝0时刻金属杆以恒定速度v＝2m/s从O点开始向右滑动。在滑动过程中保持金属杆垂直于两导轨间夹角的平分线，且与导轨接触良好。求求：（已知导轨和金属杆均足够长，sin37°＝0.6，cos37°＝0.8）

（1）在t＝6.0s时，回路中的感应电动势的大小；

（2）在t＝6.0s时，金属杆MN所受安培力的大小；

（3）在t＝6.0s时，外力对金属杆MN所做功的功率.

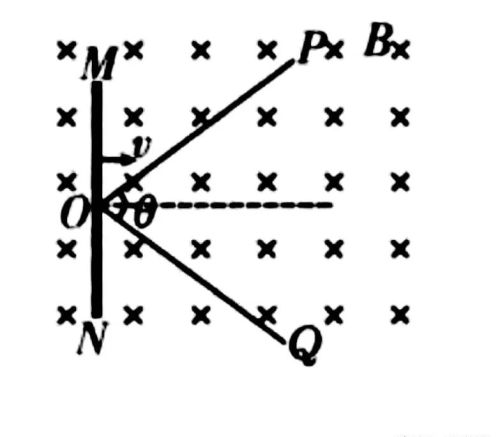
【解析】

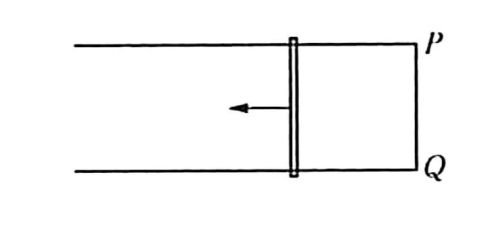
例题：如图所示，两根平行金属导轨固定在水平桌面上，每根导轨每米的电阻为r₀＝0.10Ω/m，导轨的端点P、Q用电阻可以忽略的导线相连，两导轨间的距离l＝0.20m.有随时间变化的匀强磁场垂直于桌面，已知磁感应强度B与时间t的关系为B＝kt，比例系数k＝0.020T/s.一电阻不计的金属杆可在导轨上无摩擦低滑动，在滑动过程中保持与导轨垂直.在t＝0时刻，金属杆紧靠在P、Q端，在外力作用下，杆以恒定的加速度从静止开始向导轨的另一端滑动，求在t＝6.0s时金属杆所受的安培力.

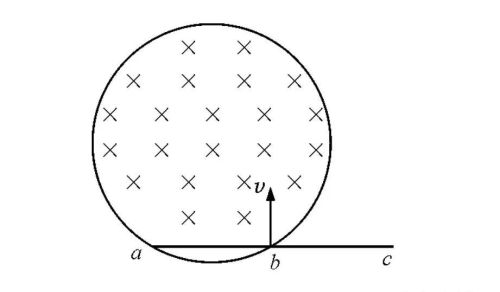
例题：如图所示，半径为R的圆形区域内有随时间变化的匀强磁场，磁感应强度B随时间t均匀增加的变化率为k ( k为常数)，t=0时的磁感应强度为B．B的方向与圆形区域垂直如图，在图中垂直纸面向内．一长为2R的金属直杆ac也处在圆形区域所在平面，并以速度v扫过磁场区域．设在t时刻杆位于图示位置，此时杆的ab段正好在磁场内，bc段位于磁场之外，且ab=bc=R，求此时杆中的感应电动势．

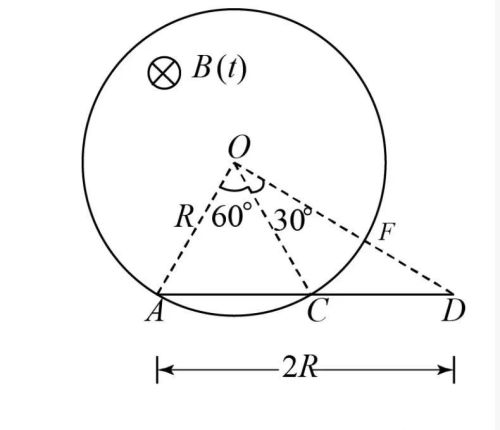
总结：

①在同时存在感生电动势与动生电动势的情况下，总电动势等于二者的代数和，二者方向相同时相加，方向相反时相减。需要注意的是，所谓方向相同或相反，是指感应电流在回路中的方向.

②单独计算感生电动势时，要取此时的回路面积；单独计算动生电动势时，要取此时的磁感应强度.

③感生和动生是相对的，也是统一的，E=N△Ф/△t是普适公式.

温馨提示：通过以上关于感生电动势和动生电动势共存现象内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。