> 情感

抛物线与相似三角形存在性问题(抛物线上三角形相似)

中考几何压轴 78 几何与函数抛物线相似三角形的存在性分类法则

中考几何压轴 78 几何与函数抛物线相似三角形的存在性分类法则

这一系列，不限专题，解析系列经典几何题，提高几何分析解决问题能力。

题85. 《相似条件求点坐标》

已知抛物线y＝ax²＋bx－4交x轴于A(-1,0),B(4,0)，交y轴于点C。

[1]. 求抛物线解析式

[2]. 如图1，P是第四象限内抛物线上一点，PA交y轴于点D，连接BD，若∠ADB＝90°，求点P的坐标；

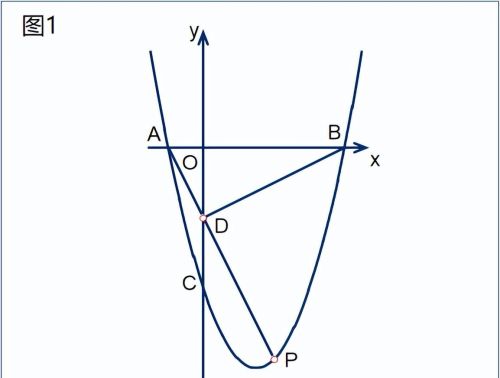
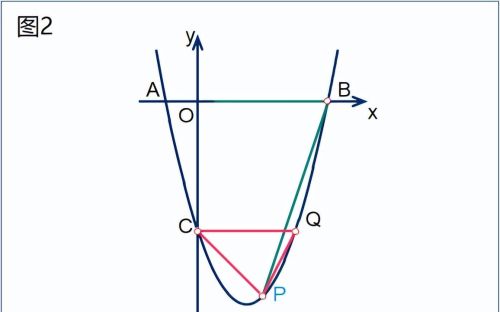
[3]. 在[2]的条件下，Q是点C关于抛物线对称轴的对称点，连接BP、CP、CQ（如图2），在x轴上是否存在点R，使得△PBR与△PQC相似？若存在，请求出点R的坐标；若不存在，请说明理由。

〖一般性提点〗

[1]. 求抛物线上点的问题

一般地，是某条直线与抛物线的交点，方法由二：

<1>. 一线三直角求点P的坐标

☆设P(t, f(t))；

☆构建一线三直角；

☆基于相似建立关于t的方程；

☆解方程并验根；

<2>. 先求直线表达式，再求直线与抛物线的交点

☆一般地，已知直线上一点

☆基于几何原理，求得直线上另一点，于是可建立直线表达式；

☆解直线、抛物线联立方程，求得交点坐标；

[2]. 相似三角形存在性的典型模式

已知定△ABC；

已知动△MNK中，M、N是定点，K某直线上动点；

已知两三角形中有一对角相等（如图），

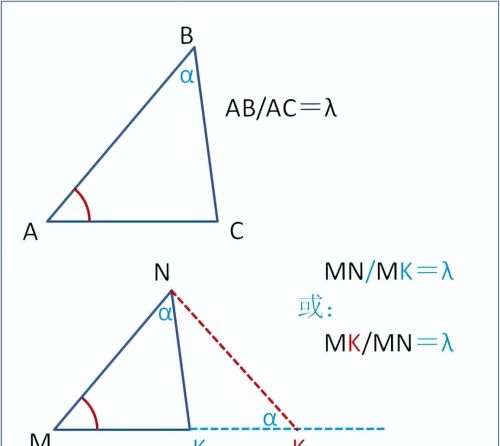
通常，确定或验证动△MNK中的定角∠NMK究竟与△ABC的哪个内角相等，是解题的关键。并优先简要探究固定三角形的性质。

〖题目分析〗

[1]. 抛物线表达式

y＝x²－3x－4＝(x＋1)(x－4)

[2]. P点坐标

<1>. 方法1：一线三直角求P点坐标：

∵ 直线AP经过抛物线零点（y＝0的点），以因式形式设P点坐标，方便求斜率：

∴设P(t, (t＋1)(t－4))；

直线AP斜率：

kAP＝(yP-yA)/(xP-xA)＝(t－4)；

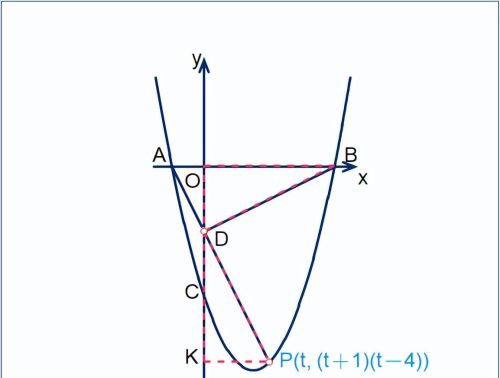
直线AP表达式：

y=kAP·(x-xA)+yA＝(t－4)(x＋1)

AP与y轴交点D(0, t－4)：

（xD=0;代入直线AP表达式：

yD=(t－4)(0＋1)；）

作PK⊥y轴于K，则如图所示，构成基于坐标轴的一线三直角结构：

OB＝4，OD＝-(t－4)＝4－t；

PK＝t，OK＝-(t＋1)(t－4)；

DK＝OK－OD＝-t (t－4)；

△PDK∽△BDO，得：

PK/OD＝DK/OB ①

各线段表达式代入①，得

(t－4)²＝4，t＝2；另一个根对应第一象限点，不符合题设，舍去；

∴ P(2,-6)为所求。

<2>. 方法2：求直线表达式，再求直线与抛物线的交点

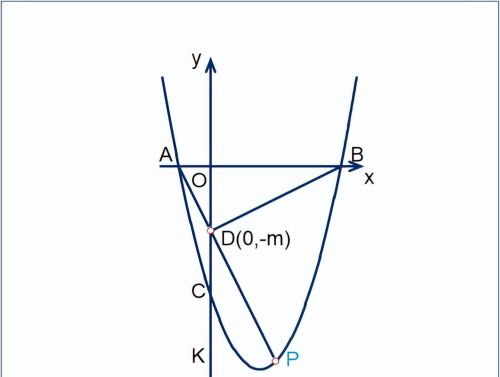
设D（0，-m）;

易知△AOD∽△BOD：OD²＝AO·BO

AO＝1；OD＝m；BO＝4

m＝2（另一根不合题设，舍去）；得

D(0,-2)

直线AD表达式y＝-2x－2；联立抛物线表达式，可解得与抛物线交点P(2,-6)；另外一解不合题意，舍去。

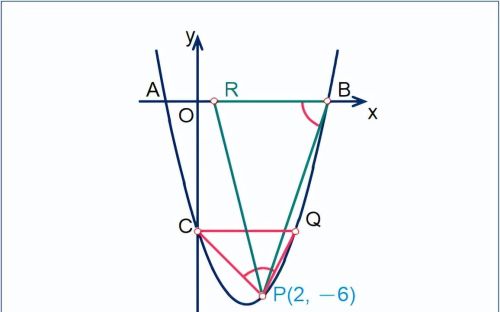
假定如图，点R为所求。

<1>. 分析角度的属性（是否定角，等）

△PBR中，∠PBR是定角；∠PBR＝△CPQ的某个内角，是两三角形相似的必要条件；

∠PBR＝∠CQP？显然，根据CQ∥OB，易知∠PBR＞∠CQP；

∠PBR＝∠QCP？比较二者大小；

为此作PK⊥CQ于K：

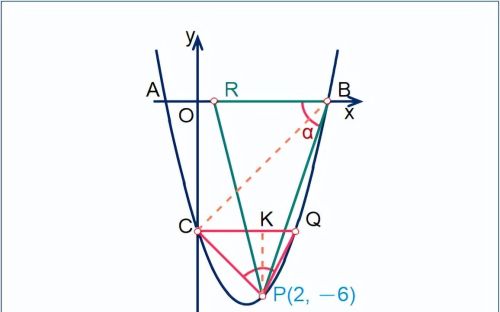
简单的计算表明：CK＝PK＝2，

∴∠QCP＝45°；

再看∠PBR，为此，连接BC，显然

∠PBR＝45°＋α＞45°，其中α＝∠PBC；

∴∠PBR＞∠QCP；

综合以上分析，△PBR∽△CPQ的必要条件是∠PBR＝∠CPQ，

<2>. 求证∠PBR＝∠CPQ

以上分析已表明，只需求证∠KPQ＝α。

为此，考察△PQK∽△BPC的条件（坐标系下，常用SAS）：

△PQK中：QK＝1；PK＝2；PK/QK＝2；∠PKQ＝90°；

△BPC中：CP＝2√2；BC＝4√2；BC/CP＝2；∠BCP＝90°；

∴△PQK∽△BPC，∠∠KPQ＝α，即

∠PBR＝∠CPQ；

<3>. 求点R(m,0)

在△PBR和△PQC中：

CP＝2√2，PQ＝√5；

PB＝2√10，RB＝4－m；

CP/PQ＝2√2/√5；

☆若PB/RB＝CP/PQ，求得：

m＝-1；

☆若RB/PB＝CP/PQ，求得：

m＝-4；

∴所求R（-1,0），或R（-4,0）。

温馨提示：通过以上关于中考几何压轴 78 几何与函数抛物线相似三角形的存在性分类法则内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。