中考压轴题数学100道抛物线(中考数学抛物线压轴题类型)

江湖救急！谁来教教老黄！这道中考数学压轴抛物线问题有点难

如图，在平面直角坐标系xOy中, 抛物线y=a(x-h)^2+k与x轴交于O,A两点, 顶点P的坐标为(2,-1). 点B为抛物线上一个动点, 连接AP, AB, 过点B的直线与抛物线交于另一点C.

(1)求抛物线的函数表达式；

(2)若点B的横坐标与纵坐标相等, ∠ABC=∠OAP, 且点C位于x轴上方, 求点C的坐标；

(3)若点B的横坐标为t, ∠ABC=90⁰, 请用含t的代数式表示点C的横坐标, 并求出t<0时, 点C的横坐标的取值范围.

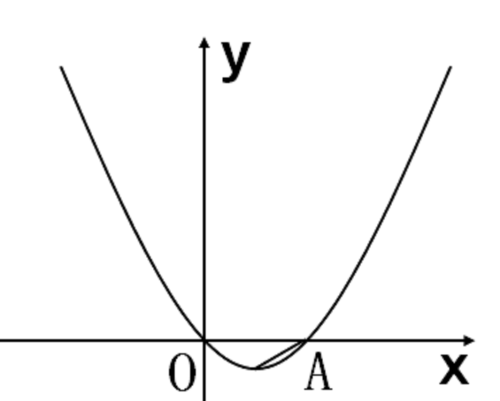
解：(1)依题意，h=2, k=-1. 【它们就是顶点的坐标，h是横坐标，k是纵坐标】

将(0,0)代入y=a(x-2)^2-1得：a=1/4.

∴函数表达式为：y=(x-2)^2/4-1. (或y=x^2/4-x) 【后者更有利于后面的运算】

(2)可设B(b,b^2/4-b)，

当b=b^2/4-b时，解得b=0或b=8.

当b=0时,B在原点上, 如图1,

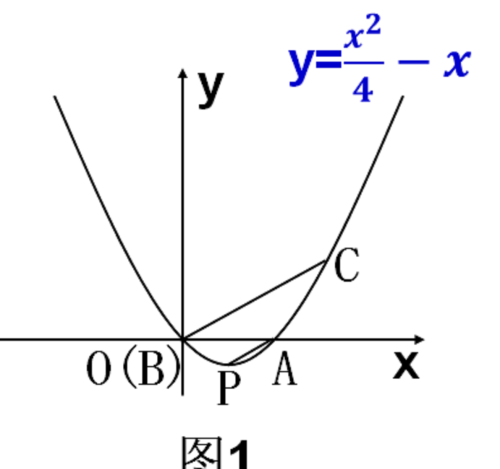
∵∠ABC=∠OAP, ∴OC//AP,

∵A(4,0), ∴直线AP的斜率为(-1)/(2-4)=1/2,

∴直线OC的解析式为y=x/2,

当x/2=x^2/4-x时,解得x=6或x=0(舍去)

∴C(6,3).

当b=8时, B(8,8)如图2, 过B作BD⊥x轴于D,

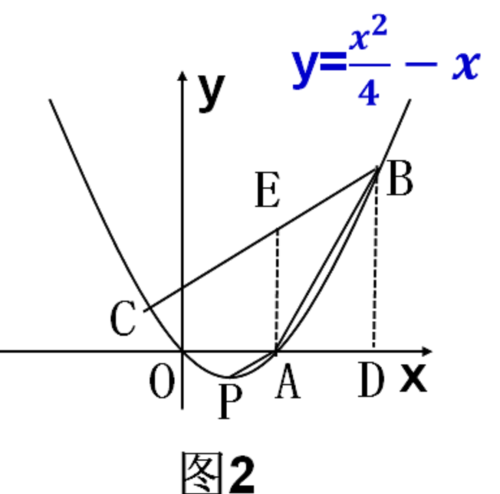
直线AB的斜率为：8/(8-4)=2,

∴∠OAP+∠BAD=90度【斜率互为倒数的两条直线与x轴的夹角互余】

∠ABD=∠OAP=∠ABC,【同角等余】

可设直线BC的解析式为y=kx+8-8k,【这里有一个代数B(8,8)求截距的过程】

过A作AE⊥x轴交BC于点E, 则E(4,8-4k),

且AE//BD, ∴∠BAE=∠ABD=∠ABC,

∴BE^2=AE^2, 即16+16k^2=(8-4k)^2, 【即BE=AE，这里用平方相等目的是避免写根式】

解得k=3/4. ∴BC的解析式为y=3x/4+2,

当x^2/4-x=3x/4+2时, 解得x=-1或x=8(舍去)，

∴C(-1,5/4)或C(6,3).

(3)如图3, B(t,t^2/4-t), (t≠4且t≠0)

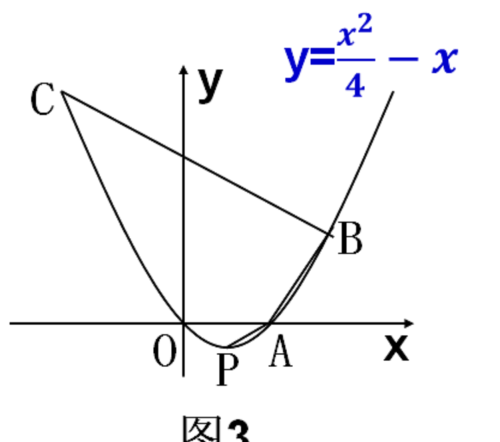
直线AB的斜率为：(t^2/4-t)/(t-4)=t/4,

∵∠ABC=90度, ∴可设BC的解析式为：y= -4x/t+p,

∴t^2/4-t=-4+p, p=t^2/4-t+4.

设C的横坐标为s,

当x^2/4-x=-4x/t+t^2/4-t+4时,

t+s=4-16/t, ∴s= -t-16/t+4, (t≠4且t≠0)【二次方程两根和公式的运用】

又s=(根号(-t)-根号(4/(-t)))^2+12≥12,

当根号(-t)=根号(4/(-t)), 即t=-4时, s=12最小.

∴点C的横坐标的取值范围为：s≥12.

相信聪明的你一定有更好的方法吧！教教老黄吧，谢谢！

更多相关：

角度有点刁钻！这道中考数学压轴关于抛物线的问题有点新！

找准切入点和角度，简便解决这道中考数学填空压轴规律题

这道中考数学题有点难度，老黄这样解对吗？请指教

温馨提示：通过以上关于江湖救急！谁来教教老黄！这道中考数学压轴抛物线问题有点难内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。